Implementing General Relativity: What's inside a black hole?

Hello! Today we’re going to do something really cool: Throw ourselves into a black hole and find out what happens. We’re going to upgrade our understanding of initial conditions via tetrads - so you can render any metric tensor - and we’re also going to learn what parallel transport is

The scope of this article is as follows:

First we’ll examine the role of coordinate systems in general relativity
Then we’ll upgrade to a black hole metric which lets us cross the event horizon
After this, we’ll learn how to calculate initial conditions for any metric tensor, instead of using pre-baked initial conditions
Then we’ll learn how to follow the path that an observer takes as it moves around spacetime - and in our case, into whatever lies inside a black hole
There will be at least one cat photo in this article

This will all be on the GPU, so it’ll run reasonably fast. We’re starting to get into things that people haven’t really simulated extensively, and this is an area where many simulations are incorrect

As always, code is available here, and you may want to read the previous article in this series first

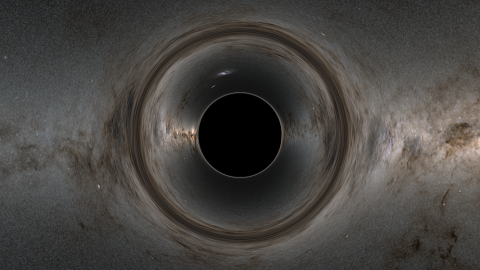
Coordinate systems

In the first article on rendering the Schwarzschild black hole, I presented you with this:

\[ds^2 = -d\tau^2 = -(1-\frac{r_s}{r}) dt^2 + (1-\frac{r_s}{r})^{-1} dr^2 + r^2 d\Omega^2\]

where $d\Omega^2 = d\theta^2 + sin^2(\theta) d\phi^2$

and called it the metric tensor for a Schwarzschild black hole. This was a white lie¹ - this is, in the more technical sense, a representation of the Schwarzschild black hole, in a particular coordinate system known as Schwarzschild coordinates. Here’s another representation:

\[ds^2 = -(1-\frac{r_s}{r}) dv^2 + 2 dvdr + r^2 d\Omega^2\]

in ingoing Eddington-Finkelstein coordinates². And another:

\[ds^2 = -d\tau^2 + \frac{r_s}{r} dp^2 + r^2 d\Omega^2\]

in Lemaître coordinates³. Note that the $d\tau$ is not proper time, its just a reuse of notation because in one specific circumstance it is proper time

The Schwarzschild black hole is an abstract object, which we can express in different coordinate systems - all of the above metrics describe the same fundamental object: a non spinning, uncharged black hole. These different coordinate systems may describe different parts of the spacetime or may have some useful mathematical properties - but there isn’t a difference in what they represent

Different coordinate systems often tend to only describe certain kinds of paths through a spacetime. For example, Schwarzschild coordinates - the one we’ve used previously - have an artificial coordinate singularity at the event horizon, which means it can’t be used to describe the motion of something that crosses the event horizon. Eddington-Finkelstein coordinates are useful for describing geodesics which are travelling forwards in time into the black hole (or equivalently, geodesics that are travelling out of the black hole backwards in time), but are singular in the opposite direction. Kruskals-Szekeres is the maximal⁴ extension of the Schwarzschild spacetime and can describe everything - though it is fairly numerically unstable. Because of the simplicity, and stability - we’re going to use ingoing eddington finkelstein coordinates today, as it covers everything we want

Coordinate transforms

If you’re wondering how exactly you interconvert these different metric tensors in different coordinate systems, this segment is for you. Otherwise skip onwards

Coordinate transforms can be done very straightforwardly. Imagine we have a coordinate system, which is $(t, r, \theta, \phi)$. We’d like to convert this to, say, $(t, x, y, z)$. Given the Schwarzschild metric, we need to substitute all the coordinates and their derivatives for the cartesian equivalents. So first up, here’s inverse of the coordinate transform

\[\begin{align} t &= t \\ r &= \sqrt{x^2 + y^2 + z^2}\\ \theta &= acos(\frac{z}{r})\\ \phi &= atan2(y, x) \end{align}\]

And then we need the inverse of the derivative of the coordinate transform, which we obtain by taking the total derivative:

\[\begin{align} dt &= dt \\ dr &= \frac{x dx + y dy + z dz}{\sqrt{x^2 + y^2 + z^2}} \\ d\theta &= \frac{z dr}{r^2 \sqrt{1 - \frac{z^2}{r^2}}} - \frac{dz}{r \sqrt{1- \frac{z^2}{r^2}}} \\ d\phi &= \frac{x dy - y dx}{x^2 + y^2} \end{align}\]

Now, all we have to do is substitute the above into the line element for Schwarzschild, which is:

\[ds^2 = -d\tau^2 = -(1-\frac{r_s}{r}) dt^2 + (1-\frac{r_s}{r})^{-1} dr^2 + r^2 d\theta^2 + r^2 sin^2(\theta) d\phi^2\]

Substituting this all through (which I am not going to do here) will give you the Schwarzschild metric in cartesian coordinates. Note that this will not give you the usually given form of the Schwarzschild metric in cartesian, as the transform is not the one we define here

Note: the metric tensor is a tensor, and the definition of a tensor is that it changes under a coordinate transform in a specific straightforward way. Its not relevant to us currently, but see here for more details if you’d like to understand this more generally

Tetrads

Back in the Schwarzschild renderer article, we learnt briefly about the role of tetrads, as objects that can be used to take a vector in our locally flat spacetime, and transform it into a vector in our curvilinear coordinate system (and vice versa):

\[v^\mu_{curved} = e^\mu_i v^i_{flat}\] \[v^i_{flat} = e_\mu^i v^\mu_{curved}\]

where $e^i_\mu = (e_i^\mu)^{-1}$ (the matrix inverse of our tetrads as column vectors)

The first thing we need to learn is how to calculate them, instead of hoping that someone else has done it for us as we’ve done previously

Calculating tetrads

As we’ve run into before: spacetime is locally flat. The technical definition of locally flat is the minkowski metric tensor $\eta_{\mu\nu}$: this is a diagonal matrix, that looks like this:

	t	x	y	z
t	-1
x		1
y			1
z				1

What we’d like to do, is mathematically define how to translate from our metric tensor $g_{\mu\nu}$, to our diagonal matrix $\eta_{\mu\nu}$ via our tetrads $e$ - and then calculate $e$. We know from general relativity that the metric must be locally⁵ diagonalisable to produce the minkowski metric (as space is locally flat, and flat = minkowski)

This is done via the standard relation:

\[D = P^{-1} A P\]

Where $D$ is our diagonal matrix, $A$ is our matrix to diagonalise, and $P$ is the diagonalising matrix. Put in our terminology⁶:

\[\eta = e^{T} g e\]

Or equivalently:

\[\eta_{ab} = g_{\mu\nu} e^\mu_a e^\nu_b\]

The metric tensor is symmetric, so the $^{-1}$ becomes a $^T$. The matrix $e$, treated as column vectors, makes up our tetrad vectors. We can solve⁷ for $e$ and get ‘a’ valid set of tetrad vectors for any metric tensor. Tetrads are not unique, so we’re just solving for the view for some arbitrary observer, that’s dependent on the specific form of the metric⁸

Solving this is an eigenvalue/vector problem, as $e$ makes up the eigenvectors of the metric (and $\eta_{\mu\nu}$ is the eigenvalues). In general relativity, one of these vectors will always have an eigenvalue of $-1$ - the timelike vector - and the other three will have an eigenvalue of $1$ - the spacelike vectors

If you have no idea what eigenvalues and eigenvectors are, its not especially important - just know that we’re appying an algorithm to solve a pretty well known class of problem

Relativistic Gram-Schmidt

The most straightforward algorithm for solving for our eigenvectors is called Gram-Schmidt Orthonormalisation⁹. Gram-Schmidt is an algorithm for taking a series of vectors and making them orthonormal to each other with respect to an inner product - which incidentally¹⁰ solves our eigenvector problem. Here we take a series of coordinate vectors, and make them orthonormal with respect to the metric tensor from each other, which produces our eigenvectors - and so our tetrads

We’re going to start off with the basic algorithm for calculating tetrads/eigenvectors, and then we’ll make it robust against the practical complexities of general relativity so you can use this a bit more generally

Lets start off with our 4 coordinate directions $v^\mu_i$, which we hope are linearly independent. $_i$ is our specific vector:

\[\begin{align} v_0 &= (1, 0, 0, 0)\\ v_1 &= (0, 1, 0, 0)\\ v_2 &= (0, 0, 1, 0)\\ v_3 &= (0, 0, 0, 1) \end{align}\]

Note that, taking the column vectors of the metric $g_{\mu\nu}$, and raising them with the metric tensor to get $v_i^\mu$ (contravariant), produces this identity matrix definitionally

For our purposes, the (modified) Gram-Schmidt algorithm looks like this:

\[\begin{align} \\ proj_{u^\mu}(v^\mu) &= \frac{g_{\mu\nu} v^\mu u^\nu}{g_{\alpha\beta} u^\alpha u^\beta} \equiv \frac{v^\mu u_\nu}{u^\alpha u_\alpha} \\ normalise(u^\mu) &= \frac{u^\mu}{g_{\alpha\beta} u^\alpha u^\beta} \equiv \frac{u^\mu}{u^\alpha u_\alpha}\\ \\ u_0 &= v_0\\ u_1 &= v_1 - proj_{u_0}(v_1) \\ \\ u_2 &= v_2 - proj_{u_0}(v_2) \\ u_2 &= u_2 - proj_{u_1}(u_2) \\ \\ u_3 &= v_3 - proj_{u_0}(v_3) \\ u_3 &= u_3 - proj_{u_1}(u_3) \\ u_3 &= u_3 - proj_{u_2}(u_3) \\ \\ u_0 &= normalise(u_0)\\ u_1 &= normalise(u_1)\\ u_2 &= normalise(u_2)\\ u_3 &= normalise(u_3)\\ \end{align}\]

Our orthonormalised vectors are $u_i^\mu$. We have to pick a vector to start our orthonormalisation from, so we pick the first vector $v_0^\mu$ arbitrarily, and now start up our algorithm:

std::array<v4f, 4> vecs = { {1, 0, 0, 0},
                            {0, 1, 0, 0},
                            {0, 0, 1, 0},
                            {0, 0, 0, 1} };

m44f metric = GetMetric(position.get());
tetrads tet = gram_schmidt(vecs[0], vecs[1], vecs[2], vecs[3], metric);

Relativistic Gram-Schmidt itself looks like this:

valuef dot(v4f u, v4f v, m44f m) {
    v4f lowered = m.lower(u);

    return dot(lowered, v);
}

v4f gram_project(v4f u, v4f v, m44f m) {
    valuef top = dot_metric(u, v, m);
    valuef bottom = dot_metric(u, u, m);

    return (top / bottom) * u;
}

v4f normalise(v4f in, m44f m)
{
    valuef d = dot_metric(in, in, m);

    //d will be < 0 for timelike vectors
    return in / sqrt(fabs(d));
}

tetrad gram_schmidt(v4f v0, v4f v1, v4f v2, v4f v3, m44f m)
{
    using namespace single_source;

    v4f u0 = v0;

    v4f u1 = v1;
    u1 = u1 - gram_project(u0, u1, m);

    //the pin()'s here are solely to cut down on compile times, and you can ignore them
    pin(u1);

    v4f u2 = v2;
    u2 = u2 - gram_project(u0, u2, m);
    u2 = u2 - gram_project(u1, u2, m);

    pin(u2);

    v4f u3 = v3;
    u3 = u3 - gram_project(u0, u3, m);
    u3 = u3 - gram_project(u1, u3, m);
    u3 = u3 - gram_project(u2, u3, m);

    pin(u3);

    u0 = normalise(u0, m);
    u1 = normalise(u1, m);
    u2 = normalise(u2, m);
    u3 = normalise(u3, m);

    pin(u0);
    pin(u1);
    pin(u2);
    pin(u3);

    return {u0, u1, u2, u3};
}

and after this, we now have our tetrads

Making this more robust

There are a few assumptions that we’ve made here

That the first vector we picked doesn’t have a length of 0, ie it isn’t null ($ds^2 = 0$)
The first vector we picked is timelike. In general, we always demand that our first tetrad $e_0$ is a timelike vector, and there’s no guarantee that $(1, 0, 0, 0)$ points in a timewards direction

Selecting the first vector

Picking the first vector is fairly straightforward: we need to loop over our vectors, and find one who’s length is not 0. Remember that in general relativity, the length of a vector is determined by

\[g_{\mu\nu} v^\mu v^\nu = v_\mu v^\mu = dot(v_\mu, v^\mu) = ds^2\]

Where $dot$ is the usual euclidian dot product

v4f v0 = {1, 0, 0, 0};
v4f v1 = {0, 1, 0, 0};
v4f v2 = {0, 0, 1, 0};
v4f v3 = {0, 0, 0, 1};

m44f metric = GetMetric(position.get());

//these are actually the column vectors of the metric tensor
v4f lv0 = metric.lower(v0);
v4f lv1 = metric.lower(v1);
v4f lv2 = metric.lower(v2);
v4f lv3 = metric.lower(v3);

array_mut<v4f> as_array = declare_mut_array_e<v4f>(4, {v0, v1, v2, v3});
//we're in theory doing v_mu v^mu, but because only one component of v0 is nonzero, and the lower components are actually
//the column vectors of the metric tensor, dot(v0, lv0) is actually metric[0,0], dot(v1, lv1) is metric[1,1] etc
//this method therefore fails if the metric has no nonzero diagonal components
array_mut<valuef> lengths = declare_mut_array_e<valuef>(4, {dot(v0, lv0), dot(v1, lv1), dot(v2, lv2), dot(v3, lv3)});

mut<valuei> first_nonzero = declare_mut_e(valuei(0));

for_e(first_nonzero < 4, assign_b(first_nonzero, first_nonzero+1), [&] {
    auto approx_eq = [](const valuef& v1, const valuef& v2) {
        valuef bound = 0.0001f;

        return v1 >= v2 - bound && v1 < v2 + bound;
    };

    if_e(!approx_eq(lengths[first_nonzero], valuef(0.f)), [&] {
            break_e();
    });
});

swap(as_array[0], as_array[first_nonzero]);

v4f iv0 = declare_e(as_array[0]);
v4f iv1 = declare_e(as_array[1]);
v4f iv2 = declare_e(as_array[2]);
v4f iv3 = declare_e(as_array[3]);

//cut down on compile times
pin(metric);

tetrad tetrads = gram_schmidt(iv0, iv1, iv2, iv3, metric);

This picks the first vector which doesn’t have a length of 0, and starts our orthonormalisation from there. You’ll also likely want to swap these tetrads back into their original positions for consistency, which we will do in the full algorithm

Picking the timelike vector, and putting it in slot 0

We know from our diagonalisation procedure, that:

\[\eta = e^{T} g e\]

$\eta$ here isn’t necessarily exactly the minkowski tensor. We’re solving an eigenvalue/vector problem, and the sign of each diagonal component (ie an eigenvalue) of $\eta$ corresponds to whether each coordinate direction at a point is timelike, or spacelike. If we use the above relation after calculating our tetrads via Gram-Schmidt, we may get this:

	?	t	?	?
?	1
t		-1
?			1
?				1

Or this:

	?	?	t	?
?	1
?		1
t			-1
?				1

Or this!

	?	?	?	t
?	1
?		1
?			1
t				-1

The reason why we list the coordinates as ?’s, is because while they correspond to cartesian coordinate directions, the specifics of which direction (x, y, or z) they are is inherently arbitrary⁸. We’re only actually able to know which one of these is time because of the signature, we don’t get any information out of this process otherwise

What we would like to do is demand that the 0’th tetrad is timelike, as this is an extremely common requirement in the literature, and it simplifies our lives tremendously when dealing with tetrads if we know that $e_0$ is timelike. Doing this means that we know that in locally flat (minkowski) coordinates, we have the coordinate system $(t, d_1, d_2, d_3)$ - which lets us construct valid geodesics straightforwardly

There are two equivalent ways of doing this:

Way the first

Calculate the minkowski metric, and find the timelike coordinate by looking for the $-1$ component

Way the second

Calculate $ ds_{i}^{2} = g_{\mu\nu} e_i^{\mu} e_i^{\nu} $, and find the component where $ds_i^2 = -1$

These are the same thing

We haven’t seen an explicit expression for how to do this the first way whereas previous articles contain plenty of the second, so we’ll pick the first

m44f get_local_minkowski(const tetrad& tetrads, const m44f& met)
{
    m44f minkowski;

    tensor<valuef, 4, 4> m;

    for(int i=0; i < 4; i++)
    {
        m[0, i] = tetrads.v[0][i];
        m[1, i] = tetrads.v[1][i];
        m[2, i] = tetrads.v[2][i];
        m[3, i] = tetrads.v[3][i];
    }

    for(int a=0; a < 4; a++)
    {
        for(int b=0; b < 4; b++)
        {
            valuef sum = 0;

            for(int mu=0; mu < 4; mu++)
            {
                for(int v=0; v < 4; v++)
                {
                    sum += met[mu, v] * m[a, mu] * m[b, v];
                }
            }

            minkowski[a, b] = sum;
        }
    }

    return minkowski;
}

valuei calculate_which_coordinate_is_timelike(const tetrad& tetrads, const m44f& met)
{
    m44f minkowski = get_local_minkowski(tetrads, met);

    using namespace single_source;

    mut<valuei> lowest_index = declare_mut_e(valuei(0));
    mut<valuef> lowest_value = declare_mut_e(valuef(0));

    for(int i=0; i < 4; i++)
    {
        if_e(minkowski[i, i] < lowest_value, [&] {
            as_ref(lowest_index) = valuei(i);
            as_ref(lowest_value) = minkowski[i, i];
        });
    }

    return lowest_index;
}

While the tetrads we get here provide a clean signature of 1’s and -1’s due to being strictly orthonormalised, we may have tetrads which are derived from numerical sources - where inaccuracy will lead to them being much less nice to work with. For this reason, we look for the largest negative value¹¹, as this is most likely to be the timelike vector

Now finally, we use the timelike coordinate to put the timelike tetrad vector in the 0th place, and end up with our final tetrads - for real this time¹². The complete procedure is therefore this:

template<auto GetMetric>
void build_initial_tetrads(execution_context& ectx, literal<v4f> position,
                           buffer_mut<v4f> position_out,
                           buffer_mut<v4f> e0_out, buffer_mut<v4f> e1_out, buffer_mut<v4f> e2_out, buffer_mut<v4f> e3_out)
{
    using namespace single_source;

    as_ref(position_out[0]) = position.get();

    v4f v0 = {1, 0, 0, 0};
    v4f v1 = {0, 1, 0, 0};
    v4f v2 = {0, 0, 1, 0};
    v4f v3 = {0, 0, 0, 1};

    m44f metric = GetMetric(position.get());

    //these are actually the column vectors of the metric tensor
    v4f lv0 = metric.lower(v0);
    v4f lv1 = metric.lower(v1);
    v4f lv2 = metric.lower(v2);
    v4f lv3 = metric.lower(v3);

    array_mut<v4f> as_array = declare_mut_array_e<v4f>(4, {v0, v1, v2, v3});
    //we're in theory doing v_mu v^mu, but because only one component of v0 is nonzero, and the lower components are actually
    //the column vectors of the metric tensor, dot(v0, lv0) is actually metric[0,0], dot(v1, lv1) is metric[1,1] etc
    //this method therefore fails if the metric has no nonzero diagonal components
    array_mut<valuef> lengths = declare_mut_array_e<valuef>(4, {dot(v0, lv0), dot(v1, lv1), dot(v2, lv2), dot(v3, lv3)});

    mut<valuei> first_nonzero = declare_mut_e(valuei(0));

    for_e(first_nonzero < 4, assign_b(first_nonzero, first_nonzero+1), [&] {
        auto approx_eq = [](const valuef& v1, const valuef& v2) {
            valuef bound = 0.0001f;

            return v1 >= v2 - bound && v1 < v2 + bound;
        };

        if_e(!approx_eq(lengths[first_nonzero], valuef(0.f)), [&] {
             break_e();
        });
    });

    swap(as_array[0], as_array[first_nonzero]);

    v4f iv0 = declare_e(as_array[0]);
    v4f iv1 = declare_e(as_array[1]);
    v4f iv2 = declare_e(as_array[2]);
    v4f iv3 = declare_e(as_array[3]);

    pin(metric);

    tetrad tetrads = gram_schmidt(iv0, iv1, iv2, iv3, metric);

    array_mut<v4f> tetrad_array = declare_mut_array_e<v4f>(4, {});

    as_ref(tetrad_array[0]) = tetrads.v[0];
    as_ref(tetrad_array[1]) = tetrads.v[1];
    as_ref(tetrad_array[2]) = tetrads.v[2];
    as_ref(tetrad_array[3]) = tetrads.v[3];

    //undo the swap we made earlier to work around null vectors
    swap(tetrad_array[0], tetrad_array[first_nonzero]);

    valuei timelike_coordinate = calculate_which_coordinate_is_timelike(tetrads, metric);

    //put the timelike vector in the 0th place
    swap(tetrad_array[0], tetrad_array[timelike_coordinate]);

    as_ref(e0_out[0]) = tetrad_array[0];
    as_ref(e1_out[0]) = tetrad_array[1];
    as_ref(e2_out[0]) = tetrad_array[2];
    as_ref(e3_out[0]) = tetrad_array[3];
}

While it may seem odd to do this on a GPU with only one thread, this procedure is identical to the one you’ll need for working with particle systems, in which case parallelising it is very handy

Following an inertial observer

So, now we have a position (our camera), and an initial tetrad. The question is: how do we follow the movements of our observer in a physically accurate way? Today we’re going to be dealing with strictly inertial observers that don’t accelerate, and we’re additionally not going to imbue our observers with any velocity - this means that they strictly will fall directly towards the black hole

The $e_0^\mu$ component of our tetrads is now always timelike - and more than that it is also (conveniently)¹³ the velocity of the observer that that tetrad represents. That is to say, if we have:

\[e_0^\mu = (1, 0, 0, 0)\]

We are dealing with an observer who’s velocity is $v^\mu = (1, 0, 0, 0)$. The first thing we need to do is to build a geodesic from our observers initial location and velocity - and then we’ll follow this geodesic along to find out where our observer ends up. Lets call these $x^{\mu}$ and $v^{\mu} = e_0^\mu$

Luckily for us, the geodesic equation for lightrays (null geodesics), and timelike geodesics, is exactly the same - which means we do not need a new equation to integrate our timelike geodesic. We’re going to need to save¹⁴ the positions and velocities of our geodesic as we trace it, so we have to modify our code a bit:

value<bool> should_terminate(v4f start, v4f position, v4f velocity)
{
    value<bool> is_broken = !isfinite(position[0]) || !isfinite(position[1]) || !isfinite(position[2]) || !isfinite(position[3]) ||
                            !isfinite(velocity[0]) || !isfinite(velocity[1]) || !isfinite(velocity[2]) || !isfinite(velocity[3]) ;

    return position[1] > 10 || position[0] > start[0] + 1000 || fabs(velocity[0]) >= 10 || is_broken || position[1] < 0.1f;
}

#define TRACE_DT 0.005f

template<auto GetMetric>
void trace_geodesic(execution_context& ectx,
                    buffer<v4f> start_position, buffer<v4f> start_velocity,
                    buffer_mut<v4f> positions_out, buffer_mut<v4f> velocity_out,
                    buffer_mut<valuei> written_steps, literal<valuei> max_steps)
{
    using namespace single_source;

    m44f metric = GetMetric(start_position[0]);

    mut<valuei> result = declare_mut_e(valuei(0));

    mut_v4f position = declare_mut_e(start_position[0]);
    mut_v4f velocity = declare_mut_e(start_velocity[0]);

    //for a timelike geodesic, dt is proper time
    float dt = TRACE_DT;
    v4f start = declare_e(start_position[0]);

    mut<valuei> idx = declare_mut_e("i", valuei(0));

    for_e(idx < 1024 * 1024 && idx < max_steps.get(), assign_b(idx, idx + 1), [&]
    {
        as_ref(positions_out[idx]) = position;
        as_ref(velocity_out[idx]) = velocity;

        v4f cposition = declare_e(position);
        v4f cvelocity = declare_e(velocity);

        v4f acceleration = calculate_acceleration_of(cposition, cvelocity, GetMetric);

        //this pin exists because it enables some optimisations for us, but has no other function
        pin(acceleration);

        as_ref(velocity) = cvelocity + acceleration * dt;
        as_ref(position) = cposition + velocity.as<valuef>() * dt;

        if_e(should_terminate(start, as_constant(position), as_constant(velocity)), [&] {
            break_e();
        });
    });

    as_ref(written_steps[0]) = idx.as_constant() + 1;
}

This procedure is very similar to our regular raytracing, but we’re writing all the positions and velocities out to a buffer. The termination condition is different now as well, as we terminate when the velocity of the geodesic is very high, or is approaching the singularity

We’ve now traced through the history of a timelike geodesic, and saved the positions and velocities so that we can examine the path that our observer takes through our spacetime. What we’d like to do now, is at a specific point along this timelike geodesic representing our observer, find out what that observer would see

The way to do this is by parallel transporting the tetrads, and using them as a basis for our observer

Parallel Transport

Parallel transport is the process of taking a vector, and moving it along a curve. The way that parallel transport works is as following: If you imagine a geodesic as a curve, and take a vector tangent to that curve, that vector’s definition relative to the curve stays constant

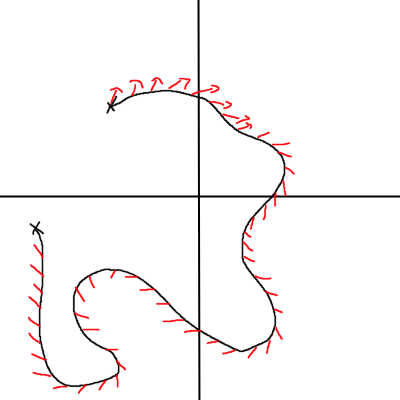
A vector which is moved along a curve in this fashion is said to be “parallel transported”. This is doable for any vector¹⁵. Note that if we have sufficient knowledge of the start and end points (specifically: we have both sets of tetrads), we can actually directly parallel transport something from the start to the end without any knowledge of the intervening path. On of this, parallel transport is path independent:

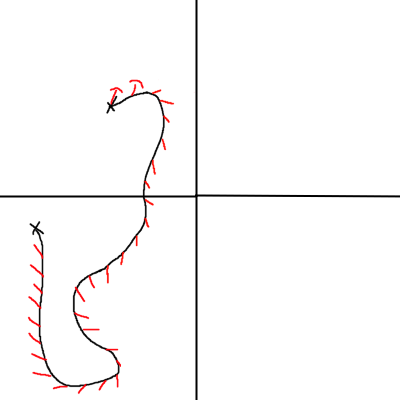
I truly am an artist

As long as the final position and velocity of the geodesic are the same¹⁶, we’ll end up with exactly the same result. Note that general relativity is torsion free - vectors do not spin around a geodesic

Parallel transport is defined as when the covariant derivative of a vector vanishes ($=0$) along a curve. We haven’t gotten around to covariant derivatives yet, but they’re the general relativistic coordinate free generalisation of partial derivatives. For more information, see this for parallel transport, and here for how to calculate covariant derivatives

For us, given a timelike geodesic parameterised by proper time, with a position $x^{\mu}$ and velocity $v^\mu = \frac{dx}{d\tau}$, the parallel transport equation for a vector $A^\mu$ is this:

\[\frac{dA^\alpha}{d\tau} = -v^\sigma \Gamma^\alpha_{\;\;\beta\sigma} A^\beta\]

In code:

v4f parallel_transport_get_change(v4f tangent_vector, v4f geodesic_velocity, const tensor<valuef, 4, 4, 4>& christoff2)
{
    v4f dAdt = {};

    for(int a=0; a < 4; a++)
    {
        valuef sum = 0;

        for(int b=0; b < 4; b++)
        {
            for(int s=0; s < 4; s++)
            {
                sum += christoff2[a,b,s] * tangent_vector[b] * geodesic_velocity[s];
            }
        }

        dAdt[a] = -sum;
    }

    return dAdt;
}

At this point, we just need to integrate this equation along our curve, and this produces our parallel transported tetrads. We’re going to build another kernel for this:

//note: we already know the value of e0, as its the geodesic velocity
template<auto GetMetric>
void parallel_transport_tetrads(execution_context& ectx, buffer<v4f> e1, buffer<v4f> e2, buffer<v4f> e3,
                                buffer<v4f> positions, buffer<v4f> velocities, buffer<valuei> counts,
                                buffer_mut<v4f> e1_out, buffer_mut<v4f> e2_out, buffer_mut<v4f> e3_out)
{
    using namespace single_source;
    //its important that this dt is the same dt as the one that we used in trace_geodesic, as we're dealing with the same parameterisation. If you use a variable timestep, you need to write this into a buffer
    float dt = TRACE_DT;

    valuei count = declare_e(counts[0]);
    mut<valuei> i = declare_mut_e(valuei(0));

    mut_v4f e1_current = declare_mut_e(e1[0]);
    mut_v4f e2_current = declare_mut_e(e2[0]);
    mut_v4f e3_current = declare_mut_e(e3[0]);

    for_e(i < count, assign_b(i, i+1), [&] {
        as_ref(e1_out[i]) = e1_current;
        as_ref(e2_out[i]) = e2_current;
        as_ref(e3_out[i]) = e3_current;

        v4f current_position = declare_e(positions[i]);
        v4f current_velocity = declare_e(velocities[i]);

        tensor<valuef, 4, 4, 4> christoff2 = calculate_christoff2(current_position, GetMetric);

        pin(christoff2);

        v4f e1_cst = declare_e(e1_current);
        v4f e2_cst = declare_e(e2_current);
        v4f e3_cst = declare_e(e3_current);

        v4f e1_change = parallel_transport_get_change(e1_cst, current_velocity, christoff2);
        v4f e2_change = parallel_transport_get_change(e2_cst, current_velocity, christoff2);
        v4f e3_change = parallel_transport_get_change(e3_cst, current_velocity, christoff2);

        as_ref(e1_current) = e1_cst + e1_change * dt;
        as_ref(e2_current) = e2_cst + e2_change * dt;
        as_ref(e3_current) = e3_cst + e3_change * dt;
    });
}

Phew. This function is a bit intentionally non compact to maximise visibillity as to what’s going on. This is a simple 1st order integrator that parallel transports the $e_{1,2,3}$ components of our tetrad, and writes them out to a buffer

You could split this up into 3 separate kernels, as the parallel transport process is fully independent for each vector. However, because we also know that these vectors are meant to be orthonormal - you could also use that fact to correct numerical integration errors here with the same Gram-Schmidt process as earlier

Interpolation

The very last thing for us to do now is to actually construct our initial conditions. If you remember, we need a position, and a set of tetrads, and that’s it for starting up our raytracing. We now have a buffer of positions, and a buffer of parallel transported tetrads - and that’s all we’re going to need to produce our initial conditions

void interpolate(execution_context& ectx, buffer<v4f> positions, buffer<v4f> e0s, buffer<v4f> e1s, buffer<v4f> e2s, buffer<v4f> e3s, buffer<valuei> counts,
                 literal<valuef> desired_proper_time,
                 buffer_mut<v4f> position_out, buffer_mut<v4f> e0_out, buffer_mut<v4f> e1_out, buffer_mut<v4f> e2_out, buffer_mut<v4f> e3_out)
{
    using namespace single_source;

    valuei size = declare_e(counts[0]);

    //somethings gone horribly wrong somewhere
    if_e(size == 0, [&] {
        return_e();
    });

    //it is again important that this timestep matches the one from parallel transported tetrads
    float dt = TRACE_DT;

    mut<valuef> elapsed_time = declare_mut_e(valuef(0));

    //fallback if we pick proper time < earliest time
    if_e(desired_proper_time.get() <= 0, [&]{
        as_ref(position_out[0]) = positions[0];
        as_ref(e0_out[0]) = e0s[0];
        as_ref(e1_out[0]) = e1s[0];
        as_ref(e2_out[0]) = e2s[0];
        as_ref(e3_out[0]) = e3s[0];

        return_e();
    });

    mut<valuei> i = declare_mut_e(valuei(0));

    //we look through our list of tetrads, and calculate the proper time T at each position
    for_e(i < (size - 1), assign_b(i, i+1), [&] {
        //if the proper time we're looking for lies between the proper times of two of our line elements
        if_e(elapsed_time >= desired_proper_time.get() && elapsed_time <= desired_proper_time.get() + dt, [&]{
            //calculate the interpolation fraction
            valuef frac = (elapsed_time - desired_proper_time.get()) / dt;

            //interpolate positions and tetrads. This might seem odd because they're in arbitrary coordinates
            //but when the ray segments are sufficiently small, this is actually a valid approximation
            as_ref(position_out[0]) = mix(positions[i], positions[i+1], frac);
            as_ref(e0_out[0]) = mix(e0s[i], e0s[i+1], frac);
            as_ref(e1_out[0]) = mix(e1s[i], e1s[i+1], frac);
            as_ref(e2_out[0]) = mix(e2s[i], e2s[i+1], frac);
            as_ref(e3_out[0]) = mix(e3s[i], e3s[i+1], frac);

            return_e();
        });

        as_ref(elapsed_time) = elapsed_time + dt;
    });

    //fallback for if we pick proper time > latest proper time
    as_ref(position_out[0]) = positions[size-1];
    as_ref(e0_out[0]) = e0s[size-1];
    as_ref(e1_out[0]) = e1s[size-1];
    as_ref(e2_out[0]) = e2s[size-1];
    as_ref(e3_out[0]) = e3s[size-1];
}

This searches for the correct proper time (the distance along our curve), and interpolates our tetrads and starting position based on whatever proper time we’re looking for. Its worth noting that with our timestep being linear, we could do this a lot more directly, but you’re likely going to have a dynamic timestep and we may as well show the full procedure here

Reviewing the complete procedure

Calculate your tetrads at a point
Ensure that $e_0$, the first tetrad vector, is timelike
Trace the timelike $e_0$ forwards, to calculate the path of our observer
Parallel transport the other vectors $e_1$ $e_2$ $e_3$ forwards along the geodesic that we define in step 3.
Calculate our final tetrad and position, by interpolating at the correct proper time along that geodesic
Raytrace using that tetrad and position¹⁷ as our initial conditions, in the usual fashion

Results

Code for this article is available here

First up, lets examine some results for Schwarzschild, in Schwarzschild coordinates. We know that the event horizon in Schwarzschild is not traversible, and so any observer attempting to cross the event horizon will hit a coordinate singularity. This isn’t a real singularity, but its worth examining anyway

The camera gets stuck on the event horizon, because the metric becomes singular. If you examine the rays, you’ll notice that their time component blows up to infinity - which causes the camera to jitter a bit as everything - and this is a technical term - explodes

Next up, we’ll look at Schwarzschild in ingoing eddington-finkelstein coordinates. For reference, that looks like this:

metric<valuef, 4, 4> metric(const tensor<valuef, 4>& position) {
    valuef rs = 1;
    valuef r = position[1];
    valuef theta = position[2];

    metric<valuef, 4, 4> m;

    m[0, 0] = -(1-rs/r);
    m[1, 0] = 1;
    m[0, 1] = 1;

    m[2, 2] = r*r;
    m[3, 3] = r*r * sin(theta)*sin(theta);

    return m;
}

These videos approach the singularity to around 10% of the Schwarzschild radius ($r=0.1$)

From the front:

Back:

Side:

(Please note that the side view suffers from inaccuracy, and shouldn’t cut off with such a hard boudary - we’ll fix this next time)

We can see that the very common idea that the universe shrinks to a point is not true, which is pretty neat to be able to disprove, and is a frequent misconception

These videos are produced using the code from this article, and are a bit limited in terms of what they can show you as they’re intended to be replicable. Particularly the side view suffers a bit, due to our slightly non ideal termination conditions - rays get cut off prematurely, and we lack the ui to be able to see things sensibly as we fall in. Here’s a better idea of what you can get with a bit of tweaking - and a user interface:

The end

In this article, we’ve looked at purely inertial observers, with whatever velocity happens to fall out of the metric. Next time round, we’re going to examine two more components of good initial conditions:

How to set up proper camera controls
How to set up observers with an initial velocity

On top of this, we’re going to set up a good variable timestep finally, which will fix a lot of the visual issues, and increase performance significantly. This will let us take a trip through Kerr, the interstellar wormhole, and go for a general examination of a few other metrics in passing. It’ll be an article where we tie up a lot of the loose ends we’ve left straggling around so far

What’s next?

These kinds of simulations are a bottomless pit, and we’ve barely scratched the surface of the kinds of things we can simulate here - after the next article we’ll have cleared the simple stuff, and we’ll finally (!) get started on numerical relativity - so we can smash some black holes together

There’s going to be an absolutely massive amount to write up, hooray! I’m considering starting a patreon for all of this at some point (and hopefully end up as a PhD student!). I’m unfortunately very poor after many many years of illness - but I’ll see how it goes. Anyway, here’s that cat I promised:

It is very common however when referring to the Schwarzschild black hole to mean in Schwarzschild coordinates. Interestingly, it wasn’t known at the outset that the different (but physically equivalent) black hole metrics that were discovered were all the same thing in different coordinate systems, and it was used as an argument against general relativity ↩
See here, be aware of the sign convention issues: this wikipedia page uses [+,-,-,-], we use [-,+,+,+] ↩
See here. Note the sign convention issues: this wikipedia page uses [+,-,-,-], we use [-,+,+,+] ↩
A maximal extension means that all geodesics can be extended indefinitely with no coordinate singularities, though there are still genuine gravitational singularities where geodesics terminate ↩
This transformation is only valid at a point, we cannot in general find a global diagonalisation of the metric. If we could, our spacetime would be trivially flat ↩
https://arxiv.org/pdf/1908.10757 2.6 ↩
In my opinion, this equation is extremely cool as applied to general relativity. It guarantees that metrics are inherently always invertible, as they are always diagonalisable. It also heavily underpins the relationship between space being locally flat, how the metric tensor is constructed, and why the minkowski metric is always in cartesian coordinates - which is at the core of how we’re able to do anything useful in a coordinate free theory. The fact that the tetrads are actually eigenvectors is also incredibly interesting - this step feels like the step that really ties together what general relativity actually is ↩
We will be doing some tricks when we implement fps camera controls to assign some physical meaning to these directions, in fairly broad circumstances ↩ ↩²
Technically we’re using the modified version for numerical stability reasons ↩
I’m sure there are likely very good and deep mathematical reasons for this, if you know why/how orthonormalisation and eigenvectors are the same thing, I’d love to know ↩
Note: when you work with parallel transported (we’ll get around to this) tetrad vectors, the signature never changes ↩
Welll… at least for this article, when you want to implement fps style camera controls, its going to get yet more complicated ↩
https://arxiv.org/pdf/1908.10757, see the section after eq 2.1, document page 6 ↩
An alternative approach would be to step the timelike geodesics forwards as we advance forwards in proper time, but its super useful to have the whole history available to us ↩
You can imagine the geodesic equation as the process of parallel transporting the velocity vector itself along the geodesic - this is in fact one definition of a geodesic (autoparallel transport) ↩
We can formalise this: If we have a set of tetrads at one position, and we parallel transport that set of tetrads along a geodesic somewhere else, we end up with a way of expressing a general transformation from vectors at point one, to point two. This forms a coordinate dependent lorentz transform, and is extremely useful. We only ever actually need to transport the tetrad vectors, and then we get everything else for free ↩
For this article, we’ve changed the kernel we use to take a tetrad from a buffer ↩

Implementing General Relativity: What's inside a black hole?

Implementing General Relativity: What's inside a black hole?

Coordinate systems

Coordinate transforms

Tetrads

Calculating tetrads

Relativistic Gram-Schmidt

Making this more robust

Selecting the first vector

Picking the timelike vector, and putting it in slot 0

Way the first

Way the second

These are the same thing

Following an inertial observer

Parallel Transport

Interpolation

Reviewing the complete procedure

Results

The end

What’s next?

results matching ""

No results matching ""