Numerical Relativity 102: Simulating fast binary black hole collisions on the GPU
Hello! Today we’re going to do one of the coolest things in all of physics in my opinion, which is simulating the collision of two black holes. Last time round, we implemented most of what we’ll need to simulate this, so today’s job is to capitalise on that and finally smash some black holes together. I’d highly recommend reading the prior article first
This article consists of three primary parts:
- Solving a new set of initial conditions for black holes, via a simple laplacian
- Implementing new boundary conditions, as our simulation is no longer periodic and has a finite extent
- Modifying the evolution equations to render them suitable for simulating binary black hole collisions
If you’re looking for someone with a lot of enthusiasm for GPU programming, and who’d rather love to do a PhD in numerical relativity - please give me a shout! 1
The code for this article is available over here

Astrophysics Context
It’s worth taking a minute to understand what a black hole actually is, and why it’s such a difficult road to simulate them numerically. In general relativity, a black hole is a stable, self supporting configuration of spacetime, which propagates itself indefinitely. It does not require any matter to support it, nor necessarily to even form it. The spacetimes we are dealing with are vacuum solutions - there’s no matter of any description here
Black holes have two primary distinguishing features compared to other compact objects:
- They have an event horizon, out of which nothing can escape
- They form a singularity at their centre. A spinning black hole has a ring singularity (ringularity), and a non spinning black hole’s singularity is a point
The event horizon itself acts completely normally in general relativity, but it is the singularity which causes problems for us. It is a true mathematical error, and we cannot simulate it by any means. Because it will always form no matter what we do2, we must come up with some method for dealing with it

(A black hole’s ringularity)
Managing the singularity
There are two primary techniques for dealing with the singularity: excision, and ‘moving punctures’
Excision
This technique is fairly common, and involves chopping out the singularity entirely - so it is not simulated. To excise the singularity correctly, you define a boundary condition inside the black hole itself, and then use one sided derivatives on the boundary. This technique works well, but involves the complexity of calculating and implementing the boundary condition - as well as defining where you should apply it
Moving punctures
This is the technique we’ll actually be using
Moving punctures involves a bit of trickery with the coordinate system - the basic idea is that we keep the coordinate system (via the lapse \(\alpha\), and shift \(\beta^i\)) away from the singularity, so that it’s never explicitly present on the simulation grid. Instead, we have a discontinuity at the singularity - and oddly enough, this discontinuity is free to move around the simulation grid (hence: moving puncture). We still simulate the entire grid however, unlike with excision
In theory we just need the appropriate gauge conditions to keep the coordinates from meeting the singularity. In practice, it’s a lot trickier than this, and it involves a lot of subtleties to get this to work in a physically accurate way. Notably, as we have a discontinuity at the singularity, differentiating across it is incorrect and produces errors. In the moving punctures technique, we rely on the causality3 of the event horizon to prevent these errors from escaping into our wider universe
Gravitational waves
The reason for doing any of this is that tools like LIGO are able to detect gravitational waves from merging compact objects. The only way to correctly reverse engineer which objects collided, is to simulate those gravitational waves ourselves via simulations like this, and then match up which set of parameters most closely reproduces our observations. This means that accuracy here is very important
To perform this matching, there’s no better way than simply bruteforcing the entire parameter space. For a pair of black holes, you have the following parameters:
| Parameter | Description |
|---|---|
| M0 | Mass |
| M1 | Mass |
| S0 | Spin axis, normalised |
| S1 | Spin axis, normalised |
| X0 | The dimensionless spin constant |
| X1 | The dimensionless spin constant |
| e | Orbital eccentricity |
This is a lot of bruteforcing to do, and it’s why non circular orbits are such a gigantic pain: it adds a whole extra dimension to bruteforce! Initially it was hoped that mergers had no eccentricity - but as far as I’m aware, this is not the case
Traditional simulations in this area can take weeks to months, which you’ll be glad to know is not going to be the case for us. It takes a few minutes per-orbit on a 6700xt, and you should be able to run this article on quite low end hardware. Note that for equal mass binary black holes with axis aligned spins, you can use an octant symmetry reduction for an 8x performance boost. For unequal mass binaries with axis aligned spins, you can use an axisymmetric reduction for a 2x boost. We’ll be avoiding both of these here, but if you have low end hardware (<= 4GB vram or a CPU), you may want to consider this
Recap
It’s been a hot minute since the last article, so this is a quick recap before we get started. We’re working in the ADM formalism, which slices up a 4d spacetime into a series of 3d slices (a ‘foliation’). An initial 3d slice (our initial conditions) is evolved forwards in time
In general relativity, spacetime is defined completely by a metric tensor $g_{\mu\nu}$, which has a value everywhere on a 4d volume. In ADM, this is split up into various pieces - and we have the following variables for every point on our 3d surface:
| Symbol | Name | Relation to normal GR | Description |
|---|---|---|---|
| $\gamma_{ij}$ | The 3-metric tensor | $g_{ij}$ | Describes curvature on the 3 surface. Symmetric |
| $K_{ij}$ | Extrinsic curvature | $\frac{1}{2 \alpha} (D_i \beta_j + D_j \beta_i - \frac{\partial g_{ij}}{\partial_t})$ | The curvature of the 3 surface with respect to the 4th dimension. Symmetric |
| $\alpha$ | Lapse | $\sqrt{-g_{00} + \beta^m \beta_m}$ | Part of the hypersurface normal, which points into the future |
| $\beta^i$ | Shift | $g_{0i}$ | The other part of the hypersurface normal, which points into the future |
Where latin indices run from 1-3, and greek indices run from 0-4. The BSSN formalism - the set of equations we’re actually using - is a decomposition of the ADM formalism. It is theoretically exactly equivalent, but much more numerically stable in practice. It has the following variables, derived from the ADM variables as follows:
| Symbol | Name | Relation to ADM | Notes |
|---|---|---|---|
| $W$ | Conformal factor | $det(\gamma_{ij})^{-\frac{1}{6}}$ | Describes the relationship between the ADM variables, and the conformal BSSN variables. $W=0$ at the singularity |
| $\tilde{\gamma}_{ij} $ | Conformal metric tensor | $W^2 \gamma_{ij}$ | Raises and lowers the indices of conformal variables. Inverted as if it were a 3x3 matrix. Symmetric, and has a unit determinant |
| $K$ | Trace of the extrinsic curvature | $\gamma^{ij} K_{ij}$ | |
| $\tilde{A}_{ij}$ | Conformal extrinsic curvature | $W^2 (K_{ij} - \frac{1}{3} \gamma_{ij} K)$ | Trace free, symmetric |
| $\tilde{\Gamma}^i$ | Conformal Christoffel symbol | $\tilde{\gamma}^{jk} \tilde{\Gamma}^i_{jk}$ | Evolved numerically despite having an analytic value from conformal variables, for stability reasons |
| $\alpha$ | Lapse | $\alpha$ | No change |
| $\beta^i$ | Shift | $\beta^i$ | No change |
There are also a number of constraints. These are:
- The algebraic constraints. \(det(\tilde{\gamma}_{ij}) = 1\), and \(\tilde{A}_{ij}\) is trace free (\(\tilde{\gamma}^{ij} \tilde{A}_{ij} = 0\)). These are enforced: see the last article for details
- The momentum and hamiltonian constraints, called \(\mathcal{M}_i\) and \(\mathcal{H}\). We damp the former, and ignore the latter
- The Christoffel symbol constraint, \(\mathcal{G}^i = \tilde{\Gamma}^i - \tilde{\gamma}^{jk} \tilde{\Gamma}^i_{jk} = 0\). This will get damped
The only general relativity you need to know for this article is:
- Raising and lowering indices
- How to calculate a covariant derivative. $D$ is the covariant derivative associated with \(\gamma_{ij}\), and \(\tilde{D}\) is the covariant derivative associated with \(\tilde{\gamma}_{ij}\)
- Tensor index notation
What’s the plan?
We need a few things to smash black holes together successfully:
- A new set of initial conditions
- New boundary conditions, ie what happens at the edge of our domain
- Some modifications to the evolution equations
Of all of these, the initial conditions are by far the most complicated part code-wise

Initial conditions
The paper we’re going to implement today is called A simple construction of initial data for multiple black holes. This represents an extremely traditional and widespread way to construct black hole initial conditions - it’s also a very good paper that you should read. There are a few things that we need to learn right off the bat:
- This doesn’t actually make black holes, it makes objects that collapse into black holes. They have no event horizon, or apparent horizon initially. This is commonly described as a wormhole collapsing into a trumpet - a trumpet being the final configuration of a black hole in numerical relativity
- There is no direct way of specifying the ‘real’/ADM mass of a black hole
- There is a maximum value of spin that can be expressed with this technique
- This works for any number of black holes
- It’s quite a noisy start. The objects we make are surrounded by gravitational waves that escape at the beginning of our simulation. This, combined with the objects collapsing into black holes, leaves a characteristic pulse in the simulation - this can cause us problems
What are we actually trying to do?
To take a step back, we’re trying to find initial values for the following ADM variables:
\[\gamma_{ij},\; K_{ij},\; \alpha,\; \beta^i\]This technique solves for \(\gamma_{ij}\) and \(K_{ij}\), and leaves us to guess $\alpha$ and $\beta^i$. Because the latter two variables are gauge variables, we can (in theory4) pick them arbitrarily. Once we have these, we can perform the BSSN decomposition on them, and then we’re done
This method falls under the class of initial conditions known as ‘conformally flat’. This means it decomposes the metric tensor into a flat conformal metric (the identity matrix in cartesian coordinates), and a conformal/scalar factor \(\psi\). It also decomposes the extrinsic curvature \(K^{ph}_{ij}\) (‘physical’, this is our \(K_{ij}\)) into a trace $K=0$, and a trace free part which this paper calls \(K_{ij}\) (and other papers often call \(\bar{A}_{ij}\)). This is called a maximal slice
Notationally, this is already a hot mess, and this is a standard issue in the field as the notation has evolved over time. Here’s the notation for what we’re doing:
| Standard Adm | Paper Notation | Meaning |
|---|---|---|
| \(\gamma_{ij}\) | \(g_{ab}^{ph}\) | The 3-metric tensor |
| \(K_{ij}\) | \(K_{ab}^{ph}\) | Extrinsic curvature |
And for the decomposition
| Our notation | Paper Notation | Definition | Meaning |
|---|---|---|---|
| \(\psi\) | $\psi$ | $\frac{1}{\alpha} + u$, though we’ll be using $\frac{1}{\alpha} + u + 1$ as explained later | The conformal factor |
| \(\bar{\gamma}_{ij}\) | \(g_{ab}\) | \(\bar{\gamma}_{ij} = \psi^{-4} \gamma_{ij}\) | The conformally flat 3-metric. The identity matrix in cartesian coordinates |
| \(\bar{A}_{ij}\) | \(K_{ab}\) | \(\bar{A}_{ij} = \psi^2 K_{ij}\) | The conformal extrinsic curvature |
Note that this has nothing to do with the BSSN conformal decomposition: it’s just the same technique applied slightly differently. The basic idea here is that when you impose conformal flatness, and maximal slicing, the momentum constraint \(\mathcal{M}_i\) becomes linear. This allows you to calculate the final (conformal) extrinsic curvature \(\bar{A}_{ij}\) as a sum of each individual black hole’s curvature. The shape of the conformal factor $\psi$ is a guess, which is then corrected to be physical via a small correction $u$, by solving the laplacian (9) + (10)
Parameters
This method has the following parameters:
| Symbol | Description |
|---|---|
| $m$ | The bare mass parameter of a black hole |
| $S^i$ | A 3-vector representing the spin (angular ADM momentum) of a black hole |
| $P^i$ | A 3-vector representing the linear momentum (ADM mass * velocity) of a black hole |
| $x^i$ | A 3-vector representing the position of a black hole in world coordinates |
Note that bare mass is not the same thing as what you’d think of as mass (here: ADM mass), it only correlates to it. See the end of the article for more details on the definition of a black hole’s mass
While we’re saving the exact testing parameters for later, if you’d like to skip ahead, we’re going to be implementing the no spin test case on page 12, in the setup section
Conformal extrinsic curvature ($\bar{A}_{ij}$)
Calculating this is straightforward. For every black hole in our spacetime, we calculate the quantity (5), and then sum over our black holes. After accumulating all of these, I store \(\bar{A}^{ab} \bar{A}_{ab}\) as a scalar
For a single black hole:
\[\begin{align} \bar{A}^{ij}_{single} &= \frac{3}{2r^2}(P^a n^b + P^b n^a - (\bar{\gamma}^{ab} - n^a n^b) P^c n_c) \\ &+ \frac{3}{r^3}(\epsilon^{acd} S_c n_d n^b + \epsilon^{bcd} S_c n_d n^a) \end{align}\]For multiple black holes:
\[\bar{A}^{ij}_{summed} = \sum_1^k \bar{A}^{ij}_{single}\]| Symbol | Meaning |
|---|---|
| $\epsilon$ | The levi civita symbol |
| $r$ | The distance in world coordinates (ie not grid coordinates) from your current position, to the black hole in question |
| $n$ | a normal vector, which is calculated as: $n^k = x^k/r$, and points away from the black hole in question |
There’s a clear problem when \(r = 0\), and the solution is to either position your black holes so this is impossible, or clamp to a small value
If you have no plans to ever work in non cartesian coordinate systems (which we don’t), the metric tensor \(\bar{\gamma}_{ij}\) is the identity matrix, and you can ignore the index positions. It raises and lowers indices as normal
Code wise: This is all straightforward to implement:
//levi-civita symbol
tensor<valuef, 3, 3, 3> get_eijk()
{
auto eijk_func = [](int i, int j, int k)
{
if((i == 0 && j == 1 && k == 2) || (i == 1 && j == 2 && k == 0) || (i == 2 && j == 0 && k == 1))
return 1;
if(i == j || j == k || k == i)
return 0;
return -1;
};
tensor<valuef, 3, 3, 3> eijk;
for(int i=0; i < 3; i++)
for(int j=0; j < 3; j++)
for(int k=0; k < 3; k++)
eijk[i, j, k] = eijk_func(i, j, k);
return eijk;
}
tensor<valuef, 3, 3> get_aIJ(v3f world_pos, v3f bh_pos, v3f angular_momentum, v3f momentum)
{
tensor<valuef, 3, 3, 3> eijk = get_eijk();
tensor<valuef, 3, 3> aij;
metric<valuef, 3, 3> flat;
for(int i=0; i < 3; i++)
{
flat[i, i] = 1;
}
for(int i=0; i < 3; i++)
{
for(int j=0; j < 3; j++)
{
valuef r = (world_pos - bh_pos).length();
r = max(r, valuef(1e-6f));
tensor<valuef, 3> n = (world_pos - bh_pos) / r;
tensor<valuef, 3> momentum_lo = flat.lower(momentum);
tensor<valuef, 3> n_lo = flat.lower(n);
aij[i, j] += (3 / (2.f * r * r)) * (momentum_lo[i] * n_lo[j] + momentum_lo[j] * n_lo[i] - (flat[i, j] - n_lo[i] * n_lo[j]) * sum_multiply(momentum, n_lo));
///spin
valuef s1 = 0;
valuef s2 = 0;
for(int k=0; k < 3; k++)
{
for(int l=0; l < 3; l++)
{
s1 += eijk[k, i, l] * angular_momentum[l] * n[k] * n_lo[j];
s2 += eijk[k, j, l] * angular_momentum[l] * n[k] * n_lo[i];
}
}
aij[i, j] += (3 / (r*r*r)) * (s1 + s2);
}
}
return aij;
}
Next up: We need the conformal factor $\psi$, which involves calculating the correction $u$
Conformal Factor ($\psi$)
The conformal factor \(\psi\) here is listed as:
\[\psi = \frac{1}{\alpha} + u\]Where $u > 1$, and $\alpha$ is:
\[\frac{1}{\alpha} = \sum^N_{i=1} \frac{m_i}{2 |\overrightarrow{r} - \overrightarrow{x}_{(i)}|}\]Note that $r$ in the bottom term is a vector representing our current grid cell’s world position. The bottom expression is twice the distance of our coordinate from our $i$’th black hole. The \(\alpha\) here has nothing to do with the gauge variable lapse also notated by $\alpha$
We’re going to deviate a little from this definition, and instead calculate the correction as:
\[\psi = \frac{1}{\alpha} + u + 1\]Where $u > 0$. This is because you have a lot more precision to work with for floating point near $0$ vs near $1$, so this lets us solve for much smaller corrections without needing to resort to double precision. This means our boundary condition will be correspondingly different ($u=0$, instead of $u=1$)
Solving for $u$
Equations (9) + (10) are a classic laplacian:
\[\begin{align} &\Delta u + \beta(1 + \alpha (u + 1))^{-7} = 0\\ &\beta = \frac{1}{8} \alpha^7 \bar{A}^{ab}\bar{A}_{ab} \end{align}\]This is the slightly more complex version of the equation. Instead, we’ll actually implement (3) directly, as is common practice (eg (18), or (13))
\[\Delta \psi + \frac{1}{8} \bar{A}^{ij} \bar{A}_{ij} \psi^{-7} = 0\]To solve this, we simply expand out the laplacian, as \(\psi = \frac{1}{\alpha} + u + 1\), and \(\Delta (\frac{1}{\alpha} + u + 1) = \Delta u\). This gives our actual form of the equation that we’ll be implementing:
\[\begin{align} &\Delta u + \frac{1}{8} \bar{A}^{ij} \bar{A}_{ij} (\frac{1}{\alpha} + u + 1)^{-7} = 0\\ \end{align}\]Solving laplacians in general
Our equations are of the form:
\[\Delta u = F(u)\]And are a standard laplacian. If you already know how to solve a laplacian, there is absolutely nothing special in this section (beyond that we’re doing it on a GPU5) and you may skip it
The boundary condition
At the edge of our grid, we need to set $u$ to something. Asymptotically, $u$ is assumed to have the form $O(\frac{1}{r})$, and at infinity in the original definition $u = 1$. This means for us, $u = 0$
Fixed point iteration / 7 point stencil
The question now is: How do you actually solve a laplacian? This segment is going to deal with the theory
A laplacian in flat 3d space (which luckily we are in) is defined as such:
\[\Delta u = \frac{\partial^2 u}{\partial x_0 ^2} + \frac{\partial^2 u}{\partial x_1 ^2} + \frac{\partial^2 u}{\partial x_2 ^2}\]Ie, it is the sum of second derivatives in each direction. Given a function $f(x)$, we can approximate the second derivative with finite difference coefficients:
\[\frac{\partial^2 f(x)}{\partial x^2} = \frac{f(x - h) - 2 f(x) + f(x + h)}{h^2}\]Where $h$ is the spacing between samples. Now, we’ll treat $u$ as a function over 3d space, ie \(u(x, y, z)\), and apply the above discretisation to \(\Delta u\):
\[\begin{align} \Delta u = &\frac{u(x - h, y, z) - 2 u(x, y, z) + u(x + h, y, z)}{h^2} + \\ &\frac{u(x, y - h, z) - 2 u(x, y, z) + u(x, y + h, z)}{h^2} + \\ &\frac{u(x, y, z - h) - 2 u(x, y, z) + u(x, y, z + h)}{h^2} \\ \end{align}\]Collecting terms, we get:
\[\begin{align} \Delta u = &\frac{u(x - h, y, z) + u(x + h, y, z)}{h^2} + \\ &\frac{u(x, y - h, z) + u(x, y + h, z)}{h^2} + \\ &\frac{u(x, y, z - h) + u(x, y, z + h)}{h^2} - \\ &\frac{6 u(x, y, z)}{h^2} \end{align}\]Our initial equation is $\Delta u = F(u)$, so lets substitute in our discretisation above, and multiply by $h^2$:
\[\begin{align} &u(x - h, y, z) + u(x + h, y, z) + \\ &u(x, y - h, z) + u(x, y + h, z) + \\ &u(x, y, z - h) + u(x, y, z + h) - \\ &6 u(x, y, z) = F(u) h^2 \end{align}\]The iterative scheme for solving a laplacian (called a 5-point stencil in 2d, or a 7-point stencil in 3d), is given by solving for $u(x, y, z)$:
\[\begin{align} u(x, y, z) = \frac{1}{6}(&u(x - h, y, z) + u(x + h, y, z) + \\ &u(x, y - h, z) + u(x, y + h, z) + \\ &u(x, y, z - h) + u(x, y, z + h) - \\ &F(u) h^2) \\ \end{align}\]Simply apply this repeatedly to a grid, and you’ve solved your laplacian. For us, \(F(u) = -\frac{1}{8} \bar{A}^{ij} \bar{A}_{ij} (\frac{1}{\alpha} + u + 1)^{-7}\) (note the minus sign)
As a basic idea, this works, and is implementable. This is the form I used for a very long time: you just iterate the above equation until the change in $u$ is sufficiently small. There are two main issues:
- It can be numerically unstable, particularly for spinning black holes
- It isn’t amazingly fast, it can take ~10s or so in some cases, which is still pretty fast
The first is solved by relaxation: Ie taking our old guess, and our new guess, and taking some fraction between the two: mix(u, nextu, 0.9f). This reduces the speed of convergence, but ameliorates numerical stability problems
With that in mind, lets have a look at our first laplacian solver:
Code
///takes a linear id, and maps it to a 3d coordinate
v3i get_coordinate(valuei id, v3i dim)
{
using namespace single_source;
valuei x = id % dim.x();
valuei y = (id / dim.x()) % dim.y();
valuei z = id / (dim.x() * dim.y());
pin(x);
pin(y);
pin(z);
return {x, y, z};
}
auto laplace_basic = [](execution_context& ectx, buffer_mut<valuef> in, buffer_mut<valuef> out,
buffer<valuef> cfl, buffer<valuef> aij_aIJ,
literal<valuef> lscale, literal<v3i> ldim,
buffer_mut<valuei> still_going, literal<valuef> relax)
{
using namespace single_source;
valuei lid = value_impl::get_global_id(0);
auto dim = ldim.get();
if_e(lid >= dim.x() * dim.y() * dim.z(), [&]{
return_e();
});
v3i pos = get_coordinate(lid, dim);
//the boundary condition is implicit and does not need to be set
//ie the buffers that we pass in are initialized to the boundary condition of 0
if_e(pos.x() == 0 || pos.y() == 0 || pos.z() == 0 ||
pos.x() == dim.x() - 1 || pos.y() == dim.y() - 1 || pos.z() == dim.z() - 1, [&] {
return_e();
});
//cfl[lid] is 1 + 1/alpha, in[lid] is our guess for u
valuef rhs = -(1.f/8.f) * pow(cfl[lid] + in[lid], -7.f) * aij_aIJ[lid];
valuef h2f0 = lscale.get() * lscale.get() * rhs;
//terms to calculate the derivatives
valuef uxm1 = in[pos - (v3i){1, 0, 0}, dim];
valuef uxp1 = in[pos + (v3i){1, 0, 0}, dim];
valuef uym1 = in[pos - (v3i){0, 1, 0}, dim];
valuef uyp1 = in[pos + (v3i){0, 1, 0}, dim];
valuef uzm1 = in[pos - (v3i){0, 0, 1}, dim];
valuef uzp1 = in[pos + (v3i){0, 0, 1}, dim];
//derivatives in each direction
valuef Xs = uxm1 + uxp1;
valuef Ys = uyp1 + uym1;
valuef Zs = uzp1 + uzm1;
//our next guess for u
valuef u0n1 = (1/6.f) * (Xs + Ys + Zs - h2f0);
//old guess for u
valuef u = in[pos, dim];
//relaxation, output
as_ref(out[lid]) = mix(u, u0n1, relax.get());
valuef etol = 1e-6f;
//set a flag if the change in our value of u is still too high
if_e(fabs(u0n1 - u) > etol, [&]{
//store a 1 in address 0
still_going.atom_xchg_e(valuei(0), valuei(1));
});
};
Note that:
- The relaxation parameter is dynamic
- We use a
still_goingparameter. This sets an atomic to1(the0is an address offset) if the change in cell value is greater than an error tolerance. This is so that we can dynamically terminate when we’ve converged enough
Red-black
A technique that gives a free 2x performance increase is red-black iteration. For a standard 2d laplacian, each grid cell only accesses it’s neighbours. We can perform a red-black colouring to demonstrate this in 2 dimensions:
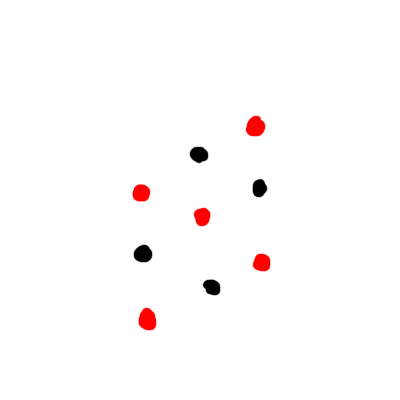
We can stretch this concept to 3 dimensions directly as well:
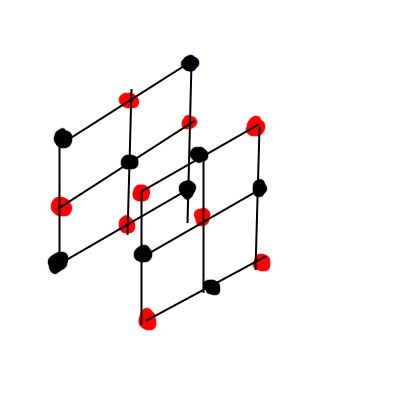
This means we can simply update all red cells, then all black cells in an alternating fashion. Because the adjacent cells are one step into the future compared to the naïve scheme, this is roughly a free 2x speedup in terms of iteration speed, and a further increase in speed due to halving the size of your problem per-iteration6. It is also more numerically stable - it’s the ultimate free lunch
There’s a slight wrinkle - our equations are not of the form \(\Delta u = 0\), but instead \(\Delta u = F(u)\). This means that we do touch a cell of the ‘wrong’ colour when updating, and it’ll be one tick out of date. That is to say, if the stencil component of our RHS is given by $D(u)$, and our iteration variable is $k$, our iteration equation is:
\[u_{k+2} = D(u_{k+1}) - \frac{F(u_k)h^2}{6}\]This does not affect convergence in practice, but it’s worth keeping in mind that this is slightly nonstandard. Code wise, red-black iteration is a simple change, and there are only two major differences:
- We can use one buffer, instead of two
- Half the threads are terminated early
auto laplace_rb_mg = [](execution_context& ectx, buffer_mut<valuef> inout, buffer<valuef> cfl, buffer<valuef> aij_aIJ,
literal<valuef> lscale, literal<v3i> ldim, literal<valuei> iteration,
buffer_mut<valuei> still_going, literal<valuef> relax)
{
using namespace single_source;
valuei lid = value_impl::get_global_id(0);
auto dim = ldim.get();
if_e(lid >= dim.x() * dim.y() * dim.z(), [&]{
return_e();
});
v3i pos = get_coordinate(lid, dim);
if_e(pos.x() == 0 || pos.y() == 0 || pos.z() == 0 ||
pos.x() == dim.x() - 1 || pos.y() == dim.y() - 1 || pos.z() == dim.z() - 1, [&] {
return_e();
});
//NEW: notice that as we offset in the z direction, our red-black scheme is simply offset in the x direction by 1
valuei lix = pos.x() + (pos.z() % 2);
valuei liy = pos.y();
//NEW!
if_e(((lix + liy) % 2) == (iteration.get() % 2), [] {
return_e();
});
valuef rhs = -(1.f/8.f) * pow(cfl[lid] + inout[lid], -7.f) * aij_aIJ[lid];
valuef h2f0 = lscale.get() * lscale.get() * rhs;
valuef uxm1 = inout[pos - (v3i){1, 0, 0}, dim];
valuef uxp1 = inout[pos + (v3i){1, 0, 0}, dim];
valuef uym1 = inout[pos - (v3i){0, 1, 0}, dim];
valuef uyp1 = inout[pos + (v3i){0, 1, 0}, dim];
valuef uzm1 = inout[pos - (v3i){0, 0, 1}, dim];
valuef uzp1 = inout[pos + (v3i){0, 0, 1}, dim];
valuef Xs = uxm1 + uxp1;
valuef Ys = uyp1 + uym1;
valuef Zs = uzp1 + uzm1;
valuef u0n1 = (1/6.f) * (Xs + Ys + Zs - h2f0);
valuef u = inout[pos, dim];
as_ref(inout[lid]) = mix(u, u0n1, relax.get());
valuef etol = 1e-6f;
if_e(fabs(u0n1 - u) > etol, [&]{
still_going.atom_xchg_e(valuei(0), valuei(1));
});
};
Sometimes, the code is simpler than the explanation! Luckily, there is no race condition with respect to $F(u)$, as we’re the only thread that both reads and modifies that value due to the red-black iteration - otherwise we’d have to use two buffers again
Multigrid
One other easy way to speed up performance is via a multigrid solution. Essentially, instead of solving at your final grid resolution, you start off at a low resolution, solve for that, and then progressively solve for higher resolutions. This is as simple as running our laplacian solving procedure at a single resolution, then upscaling that guess to a higher resolution. Do note you’ll need to re-enforce the boundary condition:
valuef get_scaled_coordinate(valuei in, valuei dimension_upper, valuei dimension_lower)
{
valuei upper_centre = (dimension_upper - 1)/2;
valuei upper_offset = in - upper_centre;
valuef scale = (valuef)(dimension_upper - 1) / (valuef)(dimension_lower - 1);
return (valuef)in / scale;
}
v3f get_scaled_coordinate_vec(v3i in, v3i dimension_upper, v3i dimension_lower)
{
v3f ret;
for(int i=0; i < 3; i++)
ret[i] = get_scaled_coordinate(in[i], dimension_upper[i], dimension_lower[i]);
return ret;
}
void upscale_buffer(execution_context& ctx, buffer<valuef> in, buffer_mut<valuef> out, literal<v3i> in_dim, literal<v3i> out_dim)
{
using namespace single_source;
valuei lid = value_impl::get_global_id(0);
auto dim = out_dim.get();
if_e(lid >= dim.x() * dim.y() * dim.z(), [&]{
return_e();
});
v3i pos = get_coordinate(lid, dim);
v3f lower_pos = get_scaled_coordinate_vec(pos, dim, in_dim.get());
if_e(pos.x() == 0 || pos.y() == 0 || pos.z() == 0 ||
pos.x() == dim.x() - 1 || pos.y() == dim.y() - 1 || pos.z() == dim.z() - 1, [&]{
return_e();
});
///trilinear interpolation
as_ref(out[pos, dim]) = buffer_read_linear(in, lower_pos, in_dim.get());
}
This solution works incredibly well for this problem, as $u$ is smooth other than at the puncture, and is a free performance win. There are no changes to the laplacian kernel here (almost as if this were planned), the only thing that we really need to worry about is the host side, and what grid resolutions to pick. I’ve found that lower grid resolutions can be somewhat numerically unstable7, so the relaxation parameter is dynamic. The code I use for generating this isn’t too complex:
std::vector<t3i> dims;
std::vector<float> relax;
int max_refinement_levels = 5;
///generate a dims array which gets progressively larger, eg
///63, 95, 127, 197, 223
///is generated in reverse
for(int i=0; i < max_refinement_levels; i++)
{
float div = pow(1.25, i + 1);
///exact params here are pretty unimportant
float rel = mix(0.7f, 0.3f, (float)i / (max_refinement_levels-1));
t3i next_dim = (t3i)((t3f)dim / div);
//i use strictly odd grid sizes
if((next_dim.x() % 2) == 0)
next_dim += (t3i){1,1,1};
dims.insert(dims.begin(), next_dim);
relax.insert(relax.begin(), rel);
}
dims.insert(dims.begin(), {51, 51, 51});
relax.insert(relax.begin(), 0.3f);
dims.push_back(dim);
relax.push_back(0.8f);
There’s probably some theory here on how to best generate grid sizes and relaxation parameters, so if you’re aware of a better scheme do let me know. None of the exact parameters here are particularly important in practice: it only matters that the last grid resolution is the one we actually want to solve for. As usual, I’m pulling out the relevant snippets here, and the full code is available here
Further performance work
At this point, I simply stopped - because the performance is much better than it needs to be, and it’ll solve within a few seconds. If you’d like further speedups, here’s where to go!
- The in and out buffers should be compacted to remove the strided memory accesses as a result of red-black iteration
- A list of active points should be provided as a buffer (or calculated), to avoid half of our threads simply immediately terminating due to red-black iteration
- 16-bit fixed point would be acceptable precision for many of the lower grid sizes especially
- The relaxation parameters are very pessimistic
Finishing up
After solving the laplacian, we have a value for $u$, which allows us to calculate \(\psi\) directly, as \(\psi = \frac{1}{\alpha} + u + 1\). From here, we can calculate our ADM variables:
\[\begin{align} \gamma_{ij} &= \psi^4 \bar{\gamma}_{ij}\\ K_{ij} &= \psi^{-2} \bar{A}_{ij} \end{align}\]Where if you remember: in cartesian coordinates, \(\bar{\gamma}_{ij}\) is the identity matrix (though really - the flat space metric). We already know how to construct our BSSN variables from here: check the recap or the last article for more details
One additional detail to add is that we’re only solving over our actual simulation area. A slighty better approach might be to solve over a very large area, and then extract just our simulation area at the end. I’ve found it doesn’t make much difference in practice, but when we start really chasing physical accuracy, we might do this
ADM mass estimation
If you’d like to estimate the ADM mass, we can do this via a standard approach, defined here (6):
\[M_i = m_i (1 + u_i + \sum_{i \neq j} \frac{m_j}{2 d_{ij}})\]Bear in mind that this paper uses the same convention for $u$ as we do. $d_{ij}$ is the world coordinate distance between our black holes
std::vector<float> extract_adm_masses(cl::context& ctx, cl::command_queue& cqueue, cl::buffer u_buf, t3i u_dim, float scale)
{
std::vector<float> ret;
///https://arxiv.org/pdf/gr-qc/0610128 6
for(const black_hole_params& bh : params_bh)
{
///Mi = mi(1 + ui + sum(m_j / 2d_ij) i != j
t3f pos = world_to_grid(bh.position, u_dim, scale);
cl::buffer u_read(ctx);
u_read.alloc(sizeof(cl_float));
cl::args args;
args.push_back(u_buf, pos, u_dim, u_read);
//trilinear interpolation of u
cqueue.exec("fetch_linear", args, {1}, {1});
float u = u_read.read<float>(cqueue).at(0);
float sum = 0;
for(const black_hole_params& bh2 : params_bh)
{
if(&bh == &bh2)
continue;
sum += bh2.bare_mass / (2 * (bh2.position - bh.position).length());
}
float adm_mass = bh.bare_mass * (1 + u + sum);
ret.push_back(adm_mass);
}
return ret;
}
This equation can be used to solve for a specific ADM mass from our bare mass parameter by binary searching
Gauge
We still don’t have an initial solution for our gauge variables however. Universally, \(\beta^i = 0\). The lapse \(\alpha\) is a tad more interesting - there are two8 main options:
- $\alpha = 1$
- $\alpha = \psi^{-2}$
Both work well and are widely used. The latter is better for black holes, but I’ve found that it tends to lead to neutron stars exploding spectacularly. We’re going to use #2 for this article, as we’re strictly dealing with black holes
Initial conditions recap
This is the end of the initial conditions now, hooray! Here is a celebratory picture of a cat:

To recap the sequence here:
- We immediately have a value for \(\bar{\gamma}_{ij}\), as it is the identity matrix
- We calculate our conformal extrinsic curvature \(\bar{A}^{ij}\) as a sum of the curvatures for individual black holes, and stash this somewhere. I also store the quantity \(\bar{A}^{ij} \bar{A}_{ij}\)9 for performance reasons in the laplacian. We never need the individual curvatures after this
- Then we solve our laplacian for $u$ - and use that to calculate $\psi$
- $\psi$ lets us calculate \(\gamma_{ij} = \psi^4 \bar{\gamma}_{ij}\) and \(K_{ij} = \psi^{-2} \bar{A}_{ij}\)
- Mission accomplished
After this, we set our gauge variables, and calculate the BSSN variables from our ADM variables
Boundary conditions
In our first go at this, our simulation was periodic and simply wrapped around the boundary - which was our boundary condition. Here, our simulation is no longer periodic, so we need a new set of boundary conditions. The simplest good-enough boundary condition is called the Sommerfeld boundary condition. This radiates away a field to the asymptotic value at the boundary as follows [2.39]:
\[\frac{\partial f}{\partial t} = -\frac{v x_i}{r} \frac{\partial f}{\partial x_i} - v \frac{f - f_0}{r}\]This is what everything means:
| Symbol | Meaning |
|---|---|
| $f$ | The value of whichever field we’re radiating |
| $x_i$ | The cell’s position in world coordinates |
| $v$ | The wave speed (usually 1) |
| $f_0$ | The asymptotic value of the field at infinity |
| $r$ | The distance from the origin in world coordinates |
| $\frac{\partial f}{\partial x_i}$ | The derivative of $f$ in each direction $\partial x_i$ |
You will need to implement the derivatives here as one sided derivatives, because we are at the boundary. This equation is applied to every tensor component separately, as if they were independent fields
Here’s a table of asymptotic values:
| Variable | $f_0$ | $v$ |
|---|---|---|
| $\tilde{\gamma}_{00} $ | 1 | 1 |
| $\tilde{\gamma}_{10} $ | 0 | 1 |
| $\tilde{\gamma}_{20} $ | 0 | 1 |
| $\tilde{\gamma}_{11} $ | 1 | 1 |
| $\tilde{\gamma}_{21} $ | 0 | 1 |
| $\tilde{\gamma}_{22} $ | 1 | 1 |
| $\tilde{A}_{ij}$ | 0 | 1 |
| $W$ | 1 | 1 |
| $K$ | 0 | 1 |
| \(\tilde{\Gamma}^i\) | 0 | 1 |
| $\alpha$ | 1 | $\sqrt{2}$ see (36) |
| $\beta^i$ | 0 | $1$ in practice, see (51) |
It’s common to use a wave speed of $v=1$ for all variables
Code wise, this is very straightforward:
//2nd order derivatives, including handling for boundary conditions
valuef diff1_boundary(single_source::buffer<valuef> in, int direction, const valuef& scale, v3i pos, v3i dim)
{
using namespace single_source;
v3i offset;
offset[direction] = 1;
derivative_data d;
d.scale = scale;
d.pos = pos;
d.dim = dim;
mut<valuef> val = declare_mut_e(valuef(0.f));
///due to padding, the boundary grid cell is actually pos == 1, and pos == dim - 2, instead of 0 and dim-1
value<bool> left = pos[direction] == 1;
value<bool> right = pos[direction] == dim[direction] - 2;
///If we're at the boundary, do one sided derivatives
if_e(left, [&]{
as_ref(val) = (-3.f * in[pos, dim] + 4 * in[pos + offset, dim] - in[pos + 2 * offset, dim]) / (2 * scale);
});
if_e(right, [&] {
as_ref(val) = (3.f * in[pos, dim] - 4 * in[pos - offset, dim] + in[pos - 2 * offset, dim]) / (2 * scale);
});
///otherwise shell out to diff1, which must handle near boundary points correctly
if_e(!(left || right), [&]{
as_ref(val) = diff1(in[pos, dim], direction, d);
});
return declare_e(val);
}
auto sommerfeld = [&](execution_context&, buffer<valuef> base, buffer<valuef> in, buffer_mut<valuef> out, literal<valuef> timestep,
literal<v3i> ldim,
literal<valuef> scale,
literal<valuef> wave_speed,
literal<valuef> asym,
buffer<v3i> positions,
literal<valuei> position_num) {
using namespace single_source;
valuei lid = value_impl::get_global_id(0);
pin(lid);
v3i dim = ldim.get();
if_e(lid >= position_num.get(), [&] {
return_e();
});
v3i pos = positions[lid];
pin(pos);
v3f world_pos = grid_to_world((v3f)pos, dim, scale.get());
valuef r = world_pos.length();
auto sommerfeld = [&](single_source::buffer<valuef> f, const valuef& f0, const valuef& v)
{
valuef sum = 0;
for(int i=0; i < 3; i++)
{
sum += world_pos[i] * diff1_boundary(f, i, scale.get(), pos, dim);
}
return (-sum - (f[pos, dim] - f0)) * (v/r);
};
valuef dt_boundary = sommerfeld(in, asym.get(), wave_speed.get());
//base + dt_boundary * timestep
as_ref(out[pos, dim]) = apply_evolution(base[pos, dim], dt_boundary, timestep.get());
};
Note that the boundary conditions lead to errors that gradually contaminate our simulation, and can cause problems over time. In general, this is often solved by simply placing them far away, but it’s a problem in longer lived simulations. There’s some discussion about alternate boundary conditions at the end of the article
There are two other components that need to have their boundary behaviour specified:
- Kreiss-Oliger dissipation. In our case, we’ll progressively reduce the order of Kreiss-Oliger as we approach the boundary
- Derivatives. Here, we reduce the order of derivatives as we approach the boundary
Kreiss-Oliger boundary
Here, we’ll simply reduce the order of Kreiss-Oliger as we approach the boundary. The implementation is straightforward:
valuei boundary_distance = distance_to_boundary(pos, dim);
//no dissipation on the boundary itself
if_e(boundary_distance == 0, [&] {
as_ref(out[lid]) = in[lid];
return_e();
});
auto do_kreiss = [&](int order)
{
as_ref(out[lid]) = in[lid] + eps.get() * kreiss_oliger_interior(in[pos, dim], order);
};
int max_kreiss = 4;
for(int i=1; i < max_kreiss; i++)
{
if_e(boundary_distance == i, [&] {
do_kreiss(i * 2);
});
}
if_e(boundary_distance >= max_kreiss, [&] {
do_kreiss(max_kreiss * 2);
});
And the interior function:
valuef kreiss_oliger_interior(valuef in, int order)
{
valuef val = 0;
for(int i=0; i < 3; i++)
{
//these are *not* divided by the scale, as it'll cancel out later
if(order == 2)
val += diff2nd(in, i);
if(order == 4)
val += diff4th(in, i);
if(order == 6)
val += diff6th(in, i);
if(order == 8)
val += diff8th(in, i);
if(order == 10)
val += diff10th(in, i);
}
int n = order;
float p = n - 1;
int sign = pow(-1, (p + 3)/2);
int divisor = pow(2, p+1);
float prefix = (float)sign / divisor;
return prefix * val;
}
Note that the prefix of $\epsilon \frac{\Delta t}{h}$ has been replaced by a single $\epsilon$ in this article. The maximum grid cell offset touched by a derivative is half the derivative rank: Eg the second derivative diff2nd has the definition:
valuef diff2nd(const valuef& in, int idx)
{
auto vars = get_differentiation_variables<3>(in, idx);
valuef p1 = vars[0] + vars[2];
return p1 - 2 * vars[1];
}
And touches cells at position +- 1, And the 10th derivative diff10th has the definition:
valuef diff10th(const valuef& in, int idx)
{
auto vars = get_differentiation_variables<11>(in, idx);
valuef p1 = vars[0] + vars[10];
valuef p2 = -10.f * vars[1] - 10.f * vars[9];
valuef p3 = 45.f * vars[2] + 45.f * vars[8];
valuef p4 = -120.f * vars[3] - 120.f * vars[7];
valuef p5 = 210.f * vars[4] + 210.f * vars[6];
valuef p6 = -252.f * vars[5];
return p1 + p2 + p3 + p4 + p5 + p6;
}
and touches cells at position +- 5
Derivative Boundary Conditions
Here, we’ll drop the derivative order (ie the precision) as we approach the boundary
valuef diff1(const valuef& in, int direction, const derivative_data& d)
{
valuef second;
{
///4th order derivatives
std::array<valuef, 5> vars = get_differentiation_variables<5>(in, direction);
valuef p1 = -vars[4] + vars[0];
valuef p2 = 8.f * (vars[3] - vars[1]);
second = (p1 + p2) / (12.f * d.scale);
}
valuef first;
{
std::array<valuef, 3> vars = get_differentiation_variables<3>(in, direction);
first = (vars[2] - vars[0]) / (2.f * d.scale);
}
valuei width = distance_to_boundary(d.pos[direction], d.dim[direction]);
return ternary(width >= 2, second, first);
}
Note that our diff1 function does not need to deal with derivatives on the boundary, as we never evaluate our evolution equations there (which is the role of Sommerfeld)
The ternary operator is being used here to avoid a conditional branch on the memory accesses, which is tremendously slow. The simulation grid is padded so that there are no out of bounds accesses
Modifying the equations
We’ve now solved the initial conditions, and implemented our boundary conditions: so we just use our equations from the last article, and hit go right?
(this is the lapse)

Unfortunately, the equations as-is cannot simulate binary black hole collisions, and we now enter a very murky area: Ad hoc modifying the equations, so that we can pull off these simulations correctly
In addition to the ‘usual’ issues, we also suffer from our own set of unique issues: Rather low grid resolution, 16-bit derivatives, as well as using 32-bit floats instead of 64-bit doubles. The latter is largely a non issue luckily, but it exacerbates numerical issues with the singularity, by giving us a smaller margin for error10
Note that all tests are conducted with a grid resolution of $213^3$, encompassing a region with a width of $30$
What’s wrong with the equations?
It took a very very long time for the field to be able to successfully simulate binary black hole collisions, and even longer to do full circular orbits. There are a variety of issues here, which we’ll now go over
- Bad gauge conditions can result in coordinate system stretching, as well as the singularity blowing up in the moving punctures technique (well, before it was discovered)
- Momentum constraint errors
- Christoffel symbol constraint errors
- Algebraic constraint errors (which we solved in the last article)
The structure of the equations we’re using are already adapted to simulating black holes by design, but older sets of equations were very numerically unstable for these problems. We’re skipping well over 40 years worth of research in this article, and it’s still a very active field
Gauge conditions
The BSSN equations contain extra degrees of freedom, and one allowance you can make is setting the variable $K=0$: this is called a maximal slicing. Maximal slicing defines a coordinate system that is known to have singularity avoiding tendencies, and is a good candidate for preventing our equations from exploding due to the presence of a singularity
Setting $K=0$ allows us to solve for the lapse via an elliptic equation (32). While elliptic equations are tricky to solve with any kind of efficiency, an approximate solution comes in the form of what is called the 1+log gauge - which will drive $K=0$ over time: see (17)
\[\partial_t \alpha = -2 \alpha K + \beta^i \partial_i \alpha\]Additionally, the shift is defined as such see (26), in what is called the gamma driver/freezing condition (as it drives the Christoffel symbol to stop evolving, see shift conditions for details):
\[\partial_t \beta^i = \frac{3}{4} \tilde{\Gamma}^i + \beta^j \partial_j \beta^i - \eta \beta^i\]$\eta$ is a free parameter that represents a gauge damping term: In general it is set to $\frac{2}{M}$, but it can also take fairly arbitrary values from $1$ to $>10$, or even vary spatially or by time. This parameter has a heavy influence on the paths of the black holes
Taken together, these two gauge conditions are called the moving puncture gauge, and are the standard choice for near equal mass11 binary black hole collisions
There are many gauge conditions
Here I’m presenting what I’d consider to be the most standard gauge conditions, but even a brief look through the papers linked above will show that there are a wide variety of gauge conditions. The most relevant notes here are:
- The \(\beta^k \partial_k\) terms are frequently dropped, as what they compensate for (a zero speed mode) is frequently addressed implicitly via kreiss-oliger dissipation
- There is an alternate two-variable from of the gamma driver equation, which appears to be strictly equivalent, but is expensive for us in terms of performance + memory
- These gauge conditions only work for relatively equal mass compact object collisions. For cosmological simulations or very unequal mass binaries, you’d again need different gauge conditions - there’s no one size fits all condition
Code
Implementing both of these gauge conditions is straightforward:
valuef get_dtgA(bssn_args& args, const derivative_data& d)
{
valuef bmdma = 0;
for(int i=0; i < 3; i++)
{
bmdma += args.gB[i] * diff1(args.gA, i, d);
}
///https://arxiv.org/pdf/gr-qc/0206072
return -2 * args.gA * args.K + bmdma;
}
tensor<valuef, 3> get_dtgB(bssn_args& args, const derivative_data& d)
{
///https://arxiv.org/pdf/gr-qc/0605030 (26)
tensor<valuef, 3> djbjbi;
for(int i=0; i < 3; i++)
{
valuef sum = 0;
for(int j=0; j < 3; j++)
{
sum += args.gB[j] * diff1(args.gB[i], j, d);
}
djbjbi[i] = sum;
}
///gauge damping parameter, commonly set to 2
float N = 2.f;
return (3/4.f) * args.cG + djbjbi - N * args.gB;
}
These gauge conditions on their own aren’t a fix for us (as we were actually already using these), but they are a very necessary component for a successful simulation
Momentum constraint errors
The momentum constraint can be damped in exactly the same form as in the previous article, via eg (4.9), and (54)
\[\begin{align} \mathcal{M_i} &= \partial_j \tilde{A}_i^j - \frac{1}{2} \tilde{\gamma}^{jk} \tilde{A}_{jk,i} + 6 \partial_j \phi \tilde{A}_i^j - \frac{2}{3} \partial_i K \\ \partial_i \phi &= -\frac{\partial_i W}{2 W} \\ \partial_t \tilde{A}_{ij} &= \partial_t \tilde{A}_{ij} + k_m \alpha \tilde{D}_{(i}\mathcal{M}_{j)} \\ \end{align}\]Note that the division by $W$ is fixed by clamping it to a small value, eg $0.0001$
Traditionally, momentum constraint violations tend to produce high frequency, self reinforcing oscillations, resulting in your simulation blowing up. With an implicit integrator this doesn’t happen, so momentum constraint damping is more about increasing correctness rather than for stability reasons. This makes it much less important for us in this construction
If you are using something like RK4, you will need this modification for stability reasons. We’ll be using it here to increase our correctness
Christoffel symbol errors
Fixing up this constraint is much more important to the long running of our sim. The traditional damping schemes are as following: (45)
\[\begin{align} s &= \mathrm{step}(\partial_m \beta^m)\\ \\ \partial_t \Gamma^i &= \partial_t \Gamma^i - (\chi s + \frac{2}{3}) \mathcal{G}^i \partial_m \beta^m\\ \end{align}\]or a similar modification: (2.22)
\[\partial_t \Gamma^i = \partial_t \Gamma^i + k_g \alpha \mathcal{G}^i \\\]Where $\chi$ > 0, and $k_g$ < 0. $\mathrm{step}$ is a function that returns $1$ if its argument is $> 0$, otherwise $0$12. We’ll be looking at the first equation primarily
Lets try it
With \(\chi = 0.5\) and \(k_m = 0.04\), and the non standard Kreiss-Oliger \(\epsilon = 0.05\) (see the end of the article for an in depth discussion), we get something that looks like this:
While we can play around with the constants a bit to adjust the results, at our resolution and scale, it’s essentially impossible to get this to work correctly. This kind of error is very common

These modifications would, in theory, work if you were using some kind of adaptive mesh refinement scheme with very high accuracy. The main point of this article series is to try and do simulations a little faster than that, so instead of relying on more compute power to fix our problems, we’re going to see if we can get a little more bang for our buck
Lets reproduce a result
Up until now I’ve been presenting this more informally to illustrate the kinds of errors we’ll run into. We’re now going to switch gears into trying to reproduce a specific result: The no spin test case from this paper. If you’d like some more test cases, check out this paper as well. These are the test parameters:
| Parameter Name | Symbol | BH 0 | BH 1 |
|---|---|---|---|
| Bare mass | $m$ | 0.483 | 0.483 |
| Momentum | $P^0$ | -0.133 | 0.133 |
| Angular momentum | $S^i$ | 0 | 0 |
| Position | $x^1$ | 3.257 | -3.257 |
| ADM mass | $M$ | 0.50513 | 0.505 |
The black holes are expected to collide at roughly T=160, after approximately 1.8 orbits. For our sim, we’ll have the following test parameters:
| Parameter | Value |
|---|---|
| Resolution | $213^3$ |
| Simulation width | $30$ |
| $h$ (ie scale) | simulation_width / (resolution.x - 1) |
| $\eta$ (the gauge damping parameter) | $2$ |
| $\epsilon$ (kreiss-oliger damping) | $0.05$ |
| $k_m$ (momentum constraint damping) | $0.04$ |
| $\chi$ (Christoffel damping) | $0.5$ |
The goal here is to demonstrate specific types of errors, the general approach that you might use to fix them, and to give you an overview of what kinds of issues you’re going to run into. Until we implement gravitational wave detection and a variety of error calculation, there’s little point trying to calibrate our sim exactly via the mk 1 eyeball, so we’re going for close-enough
Now we’ll go through how to diagnose some of our simulations problems:
- Christoffel symbol errors
- Kreiss-Oliger dissipation
- Gauge condition issues
Black Hole Inspiral Failure
Our black holes fail to inspiral correctly. One of the easiest ways to diagnose the cause, is to run the simulation with different values of $\chi$, our Christoffel symbol damping term:
$\chi = 0$
$\chi = 0.9$
While we can see that even though higher damping somewhat improves the situation, it’s clearly still borked. Part of fixing this will involve a better Christoffel damping scheme
Christoffel damping schemes
There are a variety of schemes available for improving the Christoffel symbols, of which I’m picking a few interesting ones:
| Informal Name | Modification | Notes | Source |
|---|---|---|---|
| Christoffel Substitution | \(\tilde{\Gamma}^i = \tilde{\gamma}^{jk} \tilde{\Gamma}^i_{jk}\) | Substitutes the variable \(\tilde{\Gamma}^i\) for the analytic quantity \(\tilde{\gamma}^{jk} \tilde{\Gamma}^i_{jk}\), only where \(\tilde{\Gamma}\) is not differentiated. Very widespread in the literature | After 32 |
| Christoffel lapse modification | \(\partial_t \tilde{\Gamma}^i = \partial_t \tilde{\Gamma}^i + k_{\tilde{\Gamma}} \alpha \mathcal{G}^i\) | \(k_{\tilde{\Gamma}} < 0\) | 2.22 |
| Metric Modification | \(\partial_t \tilde{\gamma}_{ij} = \partial_t \tilde{\gamma}_{ij} + k_{\gamma} \alpha \tilde{\gamma}_{k(i} \tilde{D}_{j)} \mathcal{G}^k\) | $k_{\gamma} < 0$ | 2.21, or table II |
Please note that the informal names are something I’ve purely jotted down for clarity, and are not standard names
The Christoffel substitution
This is easy enough to implement. There are only 4 instances where this substitution can be applied:
- In \(\mathcal{R}_{ij}\)
- Two in \(\partial_t \tilde{\Gamma}^i\)
- In \(\partial_t \beta^i\)
The analytic value is straightforward to calculate:
auto icY = cY.invert();
single_source::pin(icY);
tensor<valuef, 3> cG_out;
tensor<valuef, 3, 3, 3> christoff2 = christoffel_symbols_2(icY, derivs.dcY);
for(int i=0; i < 3; i++)
{
valuef sum = 0;
for(int m=0; m < 3; m++)
{
for(int n=0; n < 3; n++)
{
sum += icY[m, n] * christoff2[i, m, n];
}
}
cG_out[i] = sum;
}
return cG_out;
This modification can help to some degree:
Though not so much in our specific circumstance. In general, it tends to work better in octant symmetry, and causes problems with unequal mass binaries, but for us we’ll need to try some other options
Christoffel lapse modification
This modification is fairly easy to calculate. \(\mathcal{G}^i\) is conventionally defined as:
\[\mathcal{G}^i = \tilde{\Gamma}^i - \tilde{\gamma}^{jk} \tilde{\Gamma}^i_{jk}\]Implementation wise, we’re going to calculate \(k_{\tilde{\Gamma}} \alpha \mathcal{G}^i\)
tensor<valuef, 3> calculated_cG;
for(int i=0; i < 3; i++)
{
valuef sum = 0;
for(int m=0; m < 3; m++)
{
for(int n=0; n < 3; n++)
{
sum += icY[m, n] * christoff2[i, m, n];
}
}
calculated_cG[i] = sum;
}
tensor<valuef, 3> Gi = args.cG - calculated_cG;
float lapse_cst = -<SOME_CONSTANT>;
dtcG += lapse_cst * args.gA * Gi;
This modification has been a tricky one to try and show off. In general, either the value of lapse_cst is too small (eg see $-0.1$ below), resulting in no discernable change. Or, it’s too high, resulting in numerical instability. Combining it with and without the other modifications up until this point results in very little change
In general, my experience of this is that it’s one we can simply discard. I could have ditched this from the article entirely, but this kind of stuff will make up a very large quantity of what you’re going to run into in this area, so don’t be surprised if you test something with nice theoretical properties and it does absolutely nothing
Metric modification
For this, we’d like to calculate the following quantity:
\[k_{\gamma} \alpha \tilde{\gamma}_{k(i} \tilde{D}_{j)} \mathcal{G}^k\]Most implementations are unlikely to have the capability to directly perform a numerical derivative on \(\mathcal{G}^k\) (and even if you could, it’s a bad idea for performance)
One of the easiest ways to fix this is to perform all your derivatives, and covariant derivatives with dual numbers. While you could work it out precisely by hand (and it’s likely there’d be a performance benefit to doing so as some terms cancel out), it works well
This does however make the implementation a bit of a mess:
tensor<valuef, 3, 3> d_cGi;
//this loop purely deals with calculating the derivatives of Gi
//we already know that dGi = d(cGi - analytic value) = dcGi - d(analytic value)
//m is the differentiation direction, and the first index is always the derivative
for(int m=0; m < 3; m++)
{
//derivatives of metric tensor
tensor<dual<valuef>, 3, 3, 3> d_dcYij;
//metric tensor
unit_metric<dual<valuef>, 3, 3> d_cYij;
//fill in metric + its dual components
for(int i=0; i < 3; i++)
{
for(int j=0; j < 3; j++)
{
d_cYij[i, j].real = args.cY[i, j];
d_cYij[i, j].dual = derivs.dcY[m, i, j];
}
}
pin(d_cYij);
//metric inverse, as a dual
auto dicY = d_cYij.invert();
pin(dicY);
//fill in the metric derivatives + its dual components (the first derivatives of the metric derivatives, ie second derivatives)
for(int k=0; k < 3; k++)
{
for(int i=0; i < 3; i++)
{
for(int j=0; j < 3; j++)
{
d_dcYij[k, i, j].real = derivs.dcY[k, i, j];
d_dcYij[k, i, j].dual = diff1(derivs.dcY[k, i, j], m, d);
}
}
}
pin(d_dcYij);
//differentiate christoffel symbols
auto d_christoff2 = christoffel_symbols_2(dicY, d_dcYij);
pin(d_christoff2);
tensor<dual<valuef>, 3> dcGi_G;
for(int i=0; i < 3; i++)
{
dual<valuef> sum = 0;
for(int j=0; j < 3; j++)
{
for(int k=0; k < 3; k++)
{
sum += dicY[j, k] * d_christoff2[i, j, k];
}
}
//now we have the analytic derivative of the analytic christoffel symbol
dcGi_G[i] = sum;
}
pin(dcGi_G);
for(int i=0; i < 3; i++)
{
d_cGi[m, i] = diff1(args.cG[i], m, d) - dcGi_G[i].dual;
}
}
auto christoff2 = christoffel_symbols_2(icY, derivs.dcY);
tensor<valuef, 3> calculated_cG;
for(int i=0; i < 3; i++)
{
valuef sum = 0;
for(int m=0; m < 3; m++)
{
for(int n=0; n < 3; n++)
{
sum += icY[m, n] * christoff2[i, m, n];
}
}
calculated_cG[i] = sum;
}
pin(christoff2);
tensor<valuef, 3> Gi = args.cG - calculated_cG;
//uses the index convention 0;1
tensor<valuef, 3, 3> cD = covariant_derivative_high_vec(Gi, d_cGi, christoff2);
pin(cD);
for(int i=0; i < 3; i++)
{
for(int j=0; j < 3; j++)
{
valuef sum = 0;
for(int k=0; k < 3; k++)
{
sum += 0.5f * (args.cY[k, i] * cD[k, j] + args.cY[k, j] * cD[k, i]);
}
float cK = -<SOME_CONSTANT>;
dtcY.idx(i, j) += cK * args.gA * sum;
}
}
With the constant set to $-0.1$, we get this:
This is a significant improvement. There is still some inaccuracy here, but this is clearly a much more effective modification than any of the others we’ve tested. Because of this, we’ll be leaving this modification on in future tests. We’re going to try a few other things as well, which are modifications that have shown to be effective in the past for me
In general, there’s a bit of a balance between the different modifications. I’m trying to avoid hopping back and forth between different techniques, or repeatedly fine tuning before we’ve put all the techniques together as much as possible, but you can see how it’s tricky
Slow start lapse
The initial conditions we have aren’t actually for black holes, they’re for objects that collapse into black holes. This results in a lot of initial gauge jiggling as they collapse into black holes - particularly for the lapse - that can be bad for the health of the simulation. Because we have a low resolution and bad boundary conditions, this tends to lead to a lot of errors in the initial phase of the simulation, which can make it operate more poorly
One solution for this is the so called slow start lapse, where you essentially ease the lapse in more gradually over a period of time, eliminating the large initial lapse wave
As the gauge conditions are arbitrary, this does not (in theory) alter the correctness of the sim. The implementation of this is given by (27)
\[\partial_t \alpha = \partial_t \alpha - W (h e^{-\frac{t^2}{2 \sigma^2}}) (\alpha - W)\]| Symbol | Meaning | Value |
|---|---|---|
| $h$ | Scaling factor for the gaussian | $\frac{3}{5}$ |
| $t$ | Elapsed simulation time | $>= 0$ |
| $\sigma$ | Damping timescape | $20$ |
With this implemented, we get this result:
If you (really) squint14 you can see that the initial pulse is much reduced here, which is very nice. When we get around to making this physically accurate, this modification will help reduce the constraint errors overall
In general, this modification is a free win, so we’ll be leaving this on
Curvature adjusted Kreiss-Oliger dissipation (CAKO)
If you remember, Kreiss-Oliger is a method of damping high frequency oscillations present in your grid. The basic idea with our next modification (20) is that sharp features near the event horizon of a black hole are likely natural, and require less smoothing. This makes a certain amount of sense, and after all - if we’re trying to represent as much information on our grid as possible, removing high frequencies in high frequency areas seems like a prime candidate for wasting information
To adjust this, the authors multiply the damping strength, by the parameter $W$, thus making the damping strength virtually 0 near the event horizon. Let’s try it!
Testing this directly doesn’t work. I suspect that our simulation is too low resolution, and there are signs of numerical error - prior experience on my end is that the black holes are likely obviously borked visually15 - we just don’t have the debugging tools to observe this. Additionally, fully dropping the damping to $0$ at the singularity is liable to generate explosions16 in my experience. For us as it turns out, we do need some damping near the black holes, and instead I clamp the minimum damping to $max(W, k_{ko})$
In practice, I’ve found that this \(k_{ko}\) parameter is very dependent on grid resolution, and can be anywhere from 0.1 to 0.5, with lower resolutions needing higher values. We’re using an extremely low resolution, so we’ll need to go for $0.5$
Implementing this is extremely straightforward, and our Kreiss-Oliger step becomes:
as_ref(out[lid]) = in[lid] + eps.get() * kreiss_oliger_interior(in[pos, dim], order) * max(W[lid], valuef(0.5));
Done straightforwardly, in this test case the black holes outspiral. To make this work, I increase the Christoffel damping to \(k_{\gamma} = -0.15\), and $\chi=0.9$ This gives us a result that looks like this:
Fine tuning
So far, we’ve got a collection of different modifications, some of which have tweakable parameters. The ones we’re potentially going to adjust are:
| Symbol | Description | Current value |
|---|---|---|
| $k_{ko}$ | Minimum kreiss-oliger strength factor | $0.5$ |
| $\chi$ | Damping strength for the $\tilde{\Gamma}^i$ modification | $0.9$ |
| $h$ | Strength of the initial lapse damping | $\frac{3}{5}$ |
| $k_{\gamma}$ | Strength of the $\tilde{\gamma}_{ij}$ Christoffel damping | $-0.15$ |
| $\eta$ | Gauge Damping Parameter | $2$ |
| $\epsilon$ | Kreiss-Oliger damping strength | $0.05$ |
| $k_m$ | Momentum constraint damping | $0.04$ |
| $\beta^i \partial_i \alpha$ | Lapse advection? | On |
| $\beta^j \partial_j \beta^i$ | Shift advection? | On |
There will now be a brief intermission, while I run a whole lot of tests

So, with the following parameters:
| Symbol | Description | Current value |
|---|---|---|
| $k_{ko}$ | Minimum kreiss-oliger strength factor | $0.5$ |
| $\chi$ | Damping strength for the $\tilde{\Gamma}^i$ modification | $0.9$ |
| $h$ | Strength of the initial lapse damping | $\frac{4}{5}$ |
| $k_{\gamma}$ | Strength of the $\tilde{\gamma}_{ij}$ Christoffel damping | $-0.18$ |
| $\eta$ | Gauge Damping Parameter | $2$ |
| $\epsilon$ | Kreiss-Oliger damping strength | $0.05$ |
| $k_m$ | Momentum constraint damping | $0.04$ |
| $\beta^i \partial_i \alpha$ | Lapse advection? | On |
| $\beta^j \partial_j \beta^i$ | Shift advection? | On |
We get this:
This brings us a little closer to our target result. Further tuning beyond this is a bit pointless because we have no real metrics to actually validate that we’re making it more accurate, which is beyond the scope of this specific article. On the plus side, it doesn’t look like there’s any outspiralling which is a good sign, and it’s a miracle we’re able to get this close to our target result with such incredibly low resolution
Fun fact: When validating this article, I discovered a critical error in the boundary conditions, which means that I had to resimulate everything again. The joys!
Results
With all of this together, we’re able to replicate - close enough for the time being - the original paper, and we have now smashed black holes together pretty successfully!

There are still clearly some inaccuracies, and the fine tuning nature of the constants is ad-hoc, but it works well for such a low resolution. The inspiral looks smooth and largely monotonic (ie no sharp jumps, or outspiralling), which is ideal. It isn’t scientific grade by any means, but it’s a solid base for getting there in a future article
Just for fun, here’s a compilation of the major simulations we’ve done in this article:
Discussion
Overall, trying to get black hole paths to replicably follow sane trajectories at low resolutions has occupied a pretty major part of what I’ve worked on in general, and I’ve spent a significant amount of time on characterising this issue. In general, this article is actually by far the most difficult one of any of the articles I’m presenting, and it luckily all gets simpler from here. The moving punctures technique as a whole is slightly sketchy numerically at low resolutions: as mentioned previously, the puncture is a true discontinuity, and differentiating across it generates errors
In the literature, there are many ad-hoc techniques used with respect to the puncture, including:
- Dropping the order of Kreiss Oliger dissipation within the event horizon
- Dropping the order of differentiation within the event horizon
- Using upwinded stencils17 for differentiation with respect to the shift, which is very dissipative near the singularity where the shift vector undergoes a discontinuity
- Hiding the puncture, by placing it at the boundary between grid cells
These techniques tend to reduce errors by reducing the singularity, or reducing the size of differentiation stencils to reduce error propagation (as smaller stencils propagate information slower). In theory - errors in BSSN are causal, but this breaks down somewhat in the face of discretisation, and still relies on you having a sufficiently large event horizon. It be interesting to explore an excision technique instead, and see how it affects the inspiralling and constraint violation behaviour. Its on my infinitely long list!
The other primary source of errors for us is the boundary conditions. The simulation here has a very tight boundary, and this leads to errors that make their way inwards. Its very likely that part of our remaining inaccuracy is due to the boundary effect. Constraint preserving boundary conditions would likely help us significantly, though the literature is a bit light on how to actually implement them
In the future, we’ll be moving onto neutron stars, and N body particle simulations. It is much easier to reproduce results in the literature very exactly there, so we’ll have a lot less stress trying to make our objects go where they should do
Performance
After all this work, its probably worth mentioning the performance here, given that that’s the point of doing all of this on the GPU. All of test videos are shot in real time to make comparison easier, and we get roughly 90ms/tick (~3 minutes per orbit) on a 12GB 6700xt, which is excellent for midrange hardware18. If you’d like to investigate further performance work, here’s some places you can go:
- Momentum constraint damping costs 20ms, split about 50% between its calculation, and pulling the memory in in the evolution kernel. This could do with a significant reduction in overhead, some of which could be achieved by a better form of the constraint
- We only use two fixed point iterations. A multigrid approach would let you significantly improve the step size for minimal performance cost
- Stretching the coordinate space would mean we can distribute more resolution to the black holes, and less at the boundary - resulting in much better performance or accuracy
- There are many redundant expressions which are generated, and not fully optimised away by the compiler
- Memory accesses could be rearranged to maximise cache usage better, eg see here for some ideas
- We probably don’t need every field to be 32-bit. You could get away with 16-bit fixed point for eg the lapse and conformal factor, as they have a known range
From a technical perspective, we’re really pushing the GPU limits here. We overflow VGPRs (gpu registers), the instruction cache, and are nearly maxing out on memory bandwidth. We’re a little limited by GPU compiler issues too, so overall there is a lot of room for improvement
With all that said - I’m actually very happy with this simulation overall, both in terms of results, and the performance
Still, apparently none of this will ever be as delightful as a piece of paper in a box

Future articles
Next up, we’re going to take a step back from the difficulties of replicating results, and have a much more fun trip down the graphics and rasterisation pipeline, because the renderings in this article profoundly hurt my eyes. Depending on how things go, we’ll either then extract gravitational waves, or collide neutron stars together. Future articles should now come out a lot faster, as this one involved a huge amount of work on my end to find a reasonable formalism to present
The end
Misc Notes
This section contains pieces of information which are useful to know, but don’t really fit into the structure of the article here
Paper list
I’d highly recommend checking out many of the papers linked to in this article, as they crop up a lot in the literature once you go digging. In no particular order:
Improved numerical stability of stationary black hole evolution calculations
Modifications for numerical stability of black hole evolution
Numerical experiments of adjusted BSSN systems for controlling constraint violations
GRChombo: Numerical Relativity with Adaptive Mesh Refinement
A simple construction of initial data for multiple black holes
Calibration of Moving Puncture Simulations
Evolving a puncture black hole with fixed mesh refinement
Improved Moving-Puncture Techniques for Compact Binary Simulations
Gauge conditions for long-term numerical black hole evolutions without excision
Simple excision of a black hole in 3+1 numerical relativity
New frontiers in Numerical Relativity
Black Hole Mass Problems
There’s an unfortunate truth for black holes, which is that there is no unique definition of the mass of a black hole. It’s very easy to work out how much mass there is for something like the earth - because we can calculate how much matter is present, but black holes here are a vacuum solution - there’s no matter of any description in our spacetime. This means that we have to work out what the effect on spacetime a black hole has - equivalent to a certain amount of matter
There are multiple definitions of mass that we can use:
- Bare mass, which has no physical meaning. Higher = more mass, but that’s about it
- ADM mass, which is measured at ‘infinity’, and measures the deviation from a flat spacetime. Only valid in asymptotically flat spacetimes
- Komar mass - defined in stationary spacetimes
- Horizon mass, determined by the area of the event horizon
- Puncture mass, determined by the size of the correction factor $\psi$ at the puncture, which approximates the ADM mass
Black holes are a form of energy stored in spacetime and are a global phenomenon. Two black holes which are nearby each other store a significant amount of energy in the spacetime between them, increasing their mass (essentially further delocalising them). This makes it hard to pin down exactly how much ‘mass’ an individual black hole has in a binary pair, because they aren’t truly separate phenomena, nor are they truly local phenomena. This means that all of these definitions of mass can disagree
Despite this, its very common to use ADM mass via the puncture mass19 (as well as directly, for the entire system), and horizon mass with an approximation to its event horizon. We’re using the former here
Do be aware that many papers only give the black hole’s mass in terms of the ADM/puncture mass, and you’re expected to perform a binary search on the bare mass to achieve this
Event horizons / Marginally Outer Trapped Surface (MOTS)
True event horizon calculation requires storing the entire history of the simulation and tracing geodesics20 around in 4d, so it is uncommon as an approach. In the literature, a surface which is hoped to be equivalent/similar is used called the ‘marginally outer trapped surface’ (MOTS). This is a purely local quantity defined on a specific slice of spacetime. When calculating the black hole’s mass via horizon mass, the horizon area is generally calculated via the MOTS
Convergence issues, Kreiss Oliger, and implicit integrators
One of the difficulties with all of this is trying to prove that your code converges. The idea is, as your grid resolution goes up, your code should become more accurate - and correctly approximate the equations that you’re solving
The tricky part is that while we use scalar constants for damping factors, many of these factors are actually not resolution independent, and should really scale with some factor of the grid resolution
Kreiss-Oliger is something that has made replicating papers quite tricky for me especially, when testing different integrators at different resolutions. Kreiss-Oliger has the definition:
\[\partial_t U = \partial_t U + (-1)^{\frac{p+3}{2}} \epsilon \frac{h^p}{2^{p+1}} (\frac{\partial^{p+1}}{\partial x^{p+1}} + \frac{\partial^{p+1}}{\partial y^{p+1}} + \frac{\partial^{p+1}}{\partial z^{p+1}})U\]If we examine a specific form of this, you’ll notice that for eg second order Kreiss in a single direction, we can discretise it and expand it out as follows:
\[c \epsilon \frac{U[-1] -2 U[0] + U[1]}{h}\]Where $h$ is your spacing between grid cells, and $c$ is a constant we don’t care about. This involves a single division by the scale, as does any expanded form at any order. So as your grid resolution goes up, this blows up to infinity. With that in mind, this is something we integrate by time - so lets multiply by a timestep \(\Delta t\)
\[c \epsilon \frac{\Delta t}{h} (U[-1] -2 U[0] + U[1])\]You might recognise the $\frac{\Delta t}{h}$ term as the courant factor, which presents a bit of a problem for us
Courant Factors
If you’re unfamiliar with the concept, the core idea is that the timestep of any simulation is limited by what’s called a courant factor. It is essentially the statement that information can only propagate across your grid at a finite speed, and is defined as $\frac{\Delta t}{h} = C$. If you increase your timestep too high, you must have instability, because you’re trying to pipe information through your grid faster than your problem allows it to propagate. Similarly, if you change your grid resolution, you must also change your timestep to match. Most simulations have a constant courant factor, and automatically adjust the timestep to match at different resolutions
In any finite discretisation of a partial differential equation, Kreiss-Oliger’s strength is a multiple of the courant factor, and therefore its strength is a constant (or bounded) per step, independent of resolution or timestep21. This is all well and good, until we hit implicit integrators
We don’t have a courant factor
Equations which are implicitly integrated do not strictly have a courant factor, as they propagate information faster than with an explicit integrator. In fact, $\frac{\Delta t}{h}$ can be arbitrarily large, and is only limited by the convergence of your implicit integration technique. With an implicit integrator of sufficient quality - grid resolution, and timestep, are fully decoupled. With our current integration strategy, we have a pseudo-courant factor22 of ~2x an explicit integration scheme
This raises a tricky question: If we change the size of our grid resolution to being infinitely small, our timestep doesn’t necessarily have to change beyond practical convergence limitations. This means that Kreiss Oliger is somewhat ill defined for us, as there’s no reason that the prefix term is fixed or bounded. Effectively, our dissipation per step can be virtually anything, with the same constant $\epsilon$
To make this problem explicit, I’ve replaced \(\epsilon \frac{\Delta t}{h}\) by just a single $\epsilon$, and we’ll have to manually adjust this for different situations - which is already what I was having to do anyway. Unfortunately, this is the only simulation I’ve seen which uses fully implicit integration, so I’ve seen exactly 0 discussion of this issue in the literature23. This segment here talking about Kreiss-Oliger is intended as a discussion point about what’s actually going on here and what Kreiss-Oliger’s theoretical properties are - so if you know some more theoretically rigorous analysis, please let me know
Other boundary conditions
There are a variety of alternative boundary conditions to the Sommerfeld condition that we use
- Fixing every field to its asymptotic value at the boundary, and not evolving it. This works if your boundary is far away (as spacetime is asymptotically flat), but requires a lot of extra simulation space due to its poor quality
- Sponge constructions. This damps outgoing waves gradually. It’s easy to implement, but the sponge area must be large enough to avoid reflections, which also requires a lot of extra simulation space
- Constraint preserving boundary conditions. These are the best and allow you to place the boundaries closest to your simulation area (as they introduce the least error), but are more complex to implement
- Hybrid schemes. Some schemes assume that \(\beta^i = 0\) on the boundary, and evolve \(\tilde{\gamma}_{ij}\) freely, then use traditional boundary conditions for the other variables. I’ve never tested this and have no information on the quality of the result
- Compactification. This adjusts the coordinate system so that the grid represents the entire of (or a lot of the) the computational domain, and you have no boundary. This is nice theoretically, but in practice seems to be similar to a sponge construction, due to the effective information loss of diminishing resolution as a function of distance
Notes on formalisms
The conformal covariant BSSN formalism is in general less stable than non covariant BSSN
CCZ4 and other constraint damped formalisms don’t really help all that much with our problems here. They’re also fairly hungry in terms of performance, which makes them not a silver bullet in my experience. Its likely we’ll have an article experimenting with them in more detail, but I haven’t had tremendously good success over BSSN
-
I’m very bad at plugging myself. Contact me at icedshot@gmail.com, or if you’d like follow my bluesky at @spacejames.bsky.social. I also built a tool for rasterising generic metric tensors, which you might enjoy as well: Raytracer. Please feel free to contact me for any reason, even if you want to just chit chat or nerd out about space. ↩
-
In these articles, we’re dealing strictly with general relativity only. Singularities represent the breakdown of the theory, and the expectation is that there are not singularities inside a real black hole. Describing this accurately requires a new theory of gravity, which we don’t happen to have on hand ↩
-
In practice, this is a hugely complicated topic that is going to make our lives very difficult. It’s not that GR is incorrect about this, it’s that getting this guarantee in a numerical simulation is non trivial. While general relativity is a casual theory (where the maximum speed of causality is C), it is not a priori true as a result that errors in the BSSN formalism we use are causal. It also just so happens that - in theory - errors in BSSN are causal with the standard formalism - except we’re using some modifications. This means that theoretically we’re on slightly shakey grounds. In practice, error propagation is inherently non causal because of errors introduced by discretisation and discrete timestepping, which means we need a margin of error within our event horizon for errors to remain trapped within it ↩
-
Of course, as you can probably guess, it’s very important what their value is in practice for numerical reasons ↩
-
This is one of the cases where using a GPU provides transformational performance boost - we can get away with a much simpler implementation. In standard numerical relativity, it is common to use much more complex schemes because they have to converge in a reasonable time on a CPU ↩
-
The latter potential of the gains in the algorithm presented here are only realised on a CPU, as GPU architecture means that the culled threads are still alive and consuming resources. A less naïve execution and memory ordering would bring another 2x speedup, but in essence: it’s not really worth it after we go down the multigrid rabbithole ↩
-
Please note that I’m not super confident in this result, as it’s been a while since I explicitly tested that ↩
-
In general, these two options are the two simple options that work well, but there are a variety of alternatives ↩
-
If you’re triple checking, you raise and lower the indices of \(\bar{A}_{ij}\) with \(\bar{\gamma}_{ij}\). This is the identity matrix, so you could just ignore it ↩
-
The determinant of the metric tensor becomes degenerate if the gauge conditions aren’t quite right, leading to infinities turning up (specifically: you’ll likely find that the second derivatives of the metric blow up to infinity first). You can handle more degenerate matrices with double precision, giving the gauge conditions more time to catch up ↩
-
High mass ratio collisions are an unsolved problem. There might be a future article about exploring higher ratios, but we’d likely need adaptive mesh refinement to make a dent in that ↩
-
There are a few possible choices of modification here. The reason for the step function choice, is that the equations are only inherently unstable when \(\partial_m \beta^m > 0\), and \(\chi\) must have the same sign as that. I’ve also seen this implemented as a flat constant. You could also use $s = \chi > 0 ? 1 : -1$. In practice I’ve found it makes almost no difference ↩
-
This can be used to check the accuracy of your laplacian solver. You should be able to get very close to this value, eg $0.5045$ ↩
-
I promise in the next article this is going to look less visually horrendous ↩
-
Youtube compression also destroys any hope of this being visible in this article. Things to look out for are 1. Odd squarish formations trailing your black holes, or a bow wake, 2. The black holes becoming squished on your coordinate grid, and 3. The present of what looks like ‘ringing’ or high frequency artifacts internally to the black holes ↩
-
It’s actually a miracle that this test case doesn’t break, it’s very unusual ↩
-
A lot of the literature uses upwinded stencils. As far as I can tell, it essentially dissipates away high frequency oscillations caused by using an explicit integrator, and has no relevance for us. I’ve only ever gotten remarkably poor results from using them ↩
-
All I’m saying is that if some kind of GPU with a monstrous amount of vram and bandwidth turned up on my doorstep, I’d start working on LIGO data tomorrow ↩
-
The asymptotically flat infinity here is the puncture inside the black hole. I have no idea how this works, but apparently it does ↩
-
We’re actually going to do this in a future article, to produce accurate renderings of binary black hole collisions ↩
-
The definition seems odd to me - but I’m not arguing here that Kreiss-Oliger itself is in any way wrong. I do wish I had access to the original paper here so I could dig through the theory in more detail, but it’s behind a paywall and I can’t get ahold of it ↩
-
The fixed point iteration scheme here limits our large our timestep can be, not the stability of the equations. With 3 iterations we can increase our timestep further, and with more iterations or a completely different scheme entirely, we can arbitrarily increase the timestep ↩
-
The SXS group have tested imex stepping, which is a semi implicit scheme. They split the equations up, and solve them partially implicitly. Notably however, they do not solve the derivatives implicitly due to the computational cost, which means that this implicit scheme cannot sidestep the courant factor as with a fully implicit scheme - I suspect this is why they see only marginal benefits ↩