Implementing General Relativity: Wormholes, spinning black holes, accretion disks, and redshift
Hiyas! This article is the third in a series on rendering general relativity - if you’re unfamiliar you may want to read these articles first: one, two. We’re going to tie up some loose ends today, and dip heavily into the science behind Interstellar (mostly by accident)1. This is the last jumbo tutorial article I’m doing in this series - after this we’ll be moving onto numerical relativity, so its time to clear up a few straggler topics:
- Wormholes
- A dynamic timestep
- Workable camera controls/consistently orienting tetrads
- Observers with velocity
- Redshift
- Accretion disks
- Spinning black holes
- If there will be more cats (yes)
If you’re looking for a PhD student to work on numerical relativity, then I’d be very interested!
The full code for this article can be found here. First up: Wormholes
The Interstellar wormhole
The paper which describes Interstellar’s wormhole is this one. We want the configurable smooth version, which is described by equations (5a-c)
Given a coordinate system $(t, l, \theta, \phi)$, and the parameters $M$ = mass, $a$ = wormhole length and $p$ = throat radius:
\[\begin{align} r &= p + M(x \; atan(x) - \frac{1}{2}ln(1 + x^2)) \;\; &when \;\; &\vert l\vert > a \\ r &= p \;\; &when \;\; &\vert l\vert < a \\ x &= \frac{2(\vert l\vert - a)}{\pi M} \\ \\ ds^2 &= -(1-2\frac{M}{r}) dt^2 + \frac{dr^2}{1-2\frac{M}{r}} + r^2 (d\theta^2 + sin^2 \theta d\phi^2) \\ \end{align}\]Note that there’s a discontinuity in these equations at $\vert l\vert = a$ as given, so I swap (2) for a $ <= $ instead. Using the raytracer we’ve produced, we can translate this to code:
metric<valuef, 4, 4> get_metric(const tensor<valuef, 4>& position) {
using namespace single_source;
valuef M = 0.01;
valuef p = 1;
valuef a = 0.001f;
valuef l = position[1];
valuef x = 2 * (fabs(l) - a) / (M_PI * M);
//the analytic differentiator I've got can't handle multiple statements, so this becomes a ternary
valuef r = ternary(fabs(l) <= a,
p,
p + M * (x * atan(x) - 0.5f * log(1 + x*x)));
valuef theta = position[2];
metric<valuef, 4, 4> m;
m[0, 0] = -1;
m[1, 1] = 1;
m[2, 2] = r*r;
m[3, 3] = r*r * sin(theta)*sin(theta);
return m;
}
With almost no changes to our code (other than updating our termination conditions, as $l$ can be $< 0$), we can immediately produce a rendering of this:
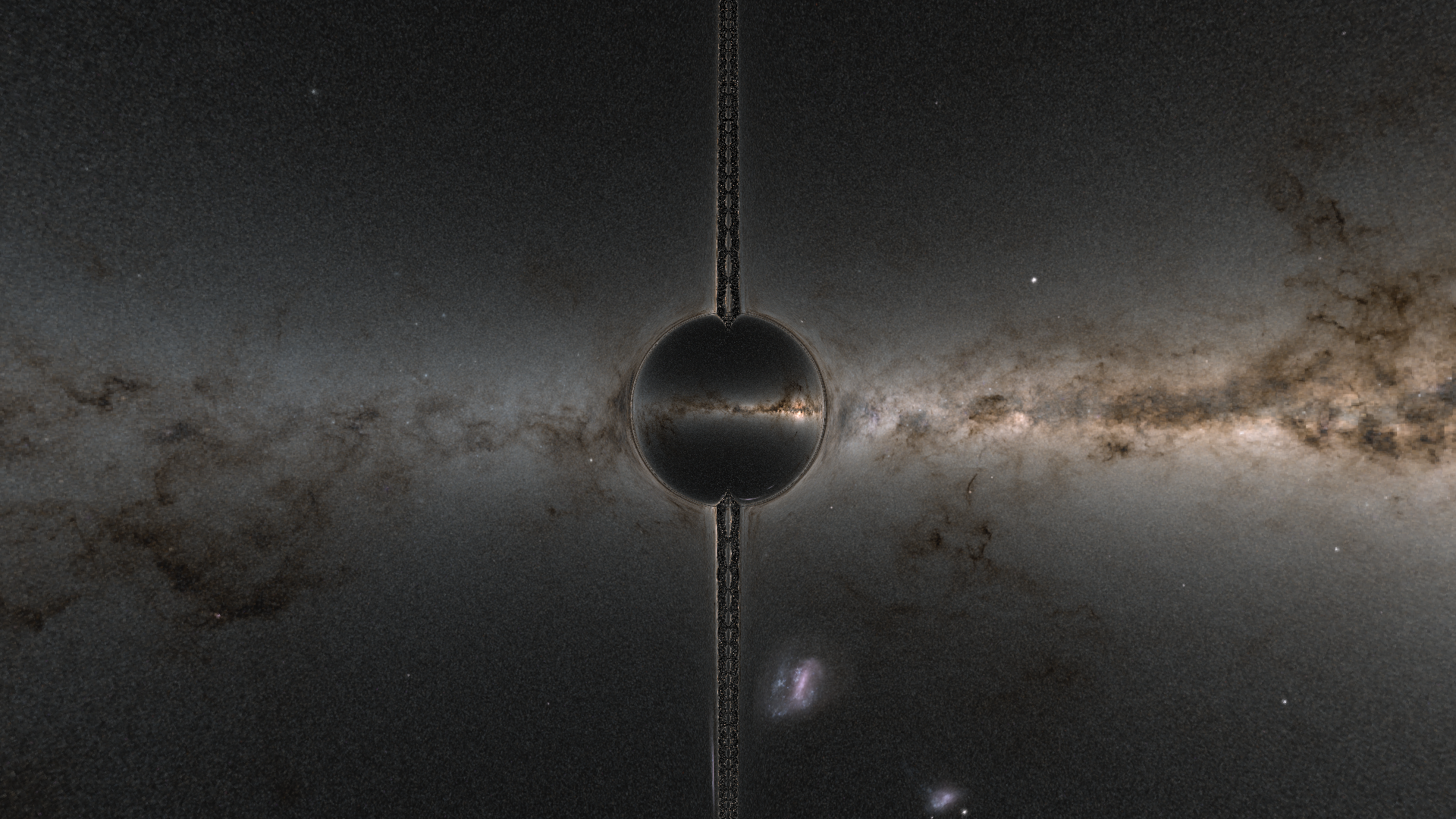
While the performance isn’t too bad at ~70ms/frame, its definitely time to fix our timestepping - particularly to cut down on spherical artifacts
Dynamic Timestepping
One of the simplest and most effective strategies for dynamic timestepping is to ensure that the distance2 a ray moves is limited to some constant. The simplest version of this method looks something like this:
valuef get_timestep(v4f position, v4f velocity)
{
v4f avelocity = fabs(velocity);
return 0.01f/max(max(avelocity.x(), avelocity.y()), max(avelocity.z(), avelocity.w()));
}
The works reasonably well, but it still gives a fairly low universal timestep, whereas we want to concentrate our timestepping more in areas that are likely to be a bit more visually interesting, ie near the object we’re simulating in question. So something like this is a bit more interesting:
valuef get_timestep(v4f position, v4f velocity)
{
v4f avelocity = fabs(velocity);
valuef divisor = max(max(avelocity.x(), avelocity.y()), max(avelocity.z(), avelocity.w()));
valuef low_precision = 0.05f/divisor;
valuef normal_precision = 0.012f/divisor;
valuef high_precision = 0.005f/divisor;
return ternary(fabs(position[1]) < 10, ternary(fabs(position[1]) < 3.f, high_precision, normal_precision), low_precision);
}
This assumes that position[1] is a radial coordinate, which is not always true - and you’ll need a generic system for calculating the distance from your object in question for this to work - but its worth it for the extra performance
With this in place, we get this result, which looks pretty great:

The singularities are barely noticable, and our performance is 60ms/frame @ 1080p. Its not incredible, but interactive framerates here are workable - more advanced timestepping and some general performance improvements can improve things a lot
Watch out for your integrator!
Be aware, not all integrators work with variable timesteps. For example, in this article we’ve previously been using the leapfrog integrator:
as_ref(velocity) = cvelocity + acceleration * dt;
as_ref(position) = cposition + velocity.as<valuef>() * dt;
Where the velocity is updated, and then the position is updated with that new velocity. This integrator does not work with a dynamic timestep, and so you must swap to a different scheme - like euler
as_ref(position) = cposition + cvelocity * dt;
as_ref(velocity) = cvelocity + acceleration * dt;
Camera Controls / Orienting Tetrads
At the moment, we’re constructing a tetrad directly from the underying metric. This works great, but results in a tetrad that - in spherical metrics - tends to point directly at our object. This leads to very unintuitive camera controls as we move our camera around. In this segment we’re going to commit some crimes against coordinate systems to get them to point roughly where we want them to
What we’d like to do is have our tetrads consistently point in a specific direction - any direction would do. While this isn’t possible to do in the general case (because the tetrads and coordinates are inherently arbitrary), as it turns out - we actually can do this in a pretty wide variety of cases
The idea here is to create an overlaying cartesian coordinate system, and use that to define our new basis vectors. Then you convert these to the real coordinate system, and orthonormalise them to produce a new set of tetrad vectors
First off, lets define what we’d like our basis vectors to be in cartesian coordinates:
\[\begin{align} b_x &= (1, 0, 0) \\ b_y &= (0, 1, 0) \\ b_z &= (0, 0, 1) \end{align}\]Now, our actual coordinate system isn’t in cartesian, so we need to convert these ideal vectors into our actual 4d coordinate system, whatever that may be. For this article everything is in spherical-like coordinates, so lets use that illustratively
\[\begin{align} t &= 0\\ r &= \sqrt{x^2 + y^2 + z^2}\\ \theta &= acos(\frac{z}{r});\\ \phi &= atan2(y, x) \end{align}\]We are dealing with tangent vectors, so we need to treat $b$ as a velocity - for that reason we want the total derivative3 of the above set of equations:
\[\begin{align} dt &= 0\\ dr &= \frac{x dx + y dy + z dz}{r}\\ d\theta &= \frac{z dr}{r^2 \sqrt{1 - \frac{z^2}{r^2}}} - \frac{dz}{r \sqrt{1 - \frac{z^2}{r^2}}}\\ d\phi &= \frac{x dy - y dx}{x^2 + y^2}\\ \end{align}\]Plug $b_k$ into these, and we’ll get a new set of vectors in our actual coordinate system that we’ll call $d_k$4. Note that we implicitly created 4-vectors from our 3-vectors here, by setting the time component to $0$
We now have 3 ($_k$) spatial vectors $d_k^\mu$, which have 4 components ($^\mu$) each. Now, calculate your tetrads as per the usual fashion, via gram-schmidt to get a valid tetrad frame $e_i^\mu$, followed by projecting your vectors $d_k^\mu$ into the local frame of reference (via the inverse tetrads). We’ll call these projected local vectors $l_k^\mu$
\[l_i^\mu = e^i_\mu d^\mu_i\]Note that $i$ ranges over 1-3. We can now orthonormalise (using normal euclidian geometry) the spatial part of these vectors ($\mu$ = 1-3) to produce a new set of basis vectors - which are now roughly oriented in the directions we picked initially ($b_k$) as best as is possible. To finish up, we turn these new 3-vectors back into spacelike 4-vectors by setting the time component to $0$, and then convert them into global coordinates with our old tetrads. These form the 3 new spacelike tetrad vectors
Only one vector is ‘true’
As you may have spotted, orthornormalising these vectors changes them - orthonormalising can only preserve the direction of a single vector (the one we start from). The correct vector to preserve is the ‘up’ vector that you use for your fixed mouse vertical axis - this means that the camera doesn’t roll as you move it around - which is very disorienting. The new vectors are still a bit of a compromise - we’re discarding the timelike component, which means that they’ll still inevitably be a bit ‘incorrect’ as to where they point - but in practice this scheme works very well
One other thing to note is that we only orient the initial tetrad if we’re parallel transporting tetrads5
Code
if(should_orient)
{
v4f spher = GenericToSpherical(position.get());
v3f cart = spherical_to_cartesian(spher.yzw());
v3f bx = (v3f){1, 0, 0};
v3f by = (v3f){0, 1, 0};
v3f bz = (v3f){0, 0, 1};
v3f sx = convert_velocity(cartesian_to_spherical, cart, bx);
v3f sy = convert_velocity(cartesian_to_spherical, cart, by);
v3f sz = convert_velocity(cartesian_to_spherical, cart, bz);
//there's an extra step here through spherical coordinates, to more consistently orient the basis when r < 0. This is optional
sx.x() = ternary(spher.y() < 0, -sx.x(), sx.x());
sy.x() = ternary(spher.y() < 0, -sy.x(), sy.x());
sz.x() = ternary(spher.y() < 0, -sz.x(), sz.x());
v4f dx = convert_velocity(SphericalToGeneric, spher, (v4f){0.f, sx.x(), sx.y(), sx.z()});
v4f dy = convert_velocity(SphericalToGeneric, spher, (v4f){0.f, sy.x(), sy.y(), sy.z()});
v4f dz = convert_velocity(SphericalToGeneric, spher, (v4f){0.f, sz.x(), sz.y(), sz.z()});
//invert the tetrads we get from the gram-schmidt process, calculated in the usual fashion
inverse_tetrad itet = tet.invert();
v4f lx = itet.into_frame_of_reference(dx);
v4f ly = itet.into_frame_of_reference(dy);
v4f lz = itet.into_frame_of_reference(dz);
//start normalising at the y coordinate, which I define as 'up' arbitrarily
std::array<v3f, 3> ortho = orthonormalise(ly.yzw(), lx.yzw(), lz.yzw());
//undo the permutation above
v4f x_basis = {0, ortho[1].x(), ortho[1].y(), ortho[1].z()};
v4f y_basis = {0, ortho[0].x(), ortho[0].y(), ortho[0].z()};
v4f z_basis = {0, ortho[2].x(), ortho[2].y(), ortho[2].z()};
v4f x_out = tet.into_coordinate_space(x_basis);
v4f y_out = tet.into_coordinate_space(y_basis);
v4f z_out = tet.into_coordinate_space(z_basis);
tet.v[1] = x_out;
tet.v[2] = y_out;
tet.v[3] = z_out;
}
Results
This results in your metric looking like this as you fly around, making it way easier to implement camera controls, as now you have a consistent usable tetrad basis
Observers with velocity / Lorentz boosts
The interstellar wormhole has neglegible gravity, so we’ll simply sit still forever if we can’t represent a moving observer. Ideally we’d like to give our observer a push in a particular direction, to represent them moving. Note that we define this velocity relative to our initial frame of reference
In a previous article, we learnt that given a set of tetrad vectors $e_i^\mu$, the 0th vector $e_0^\mu$ represents the velocity of our observer. If we want to represent an observer with a different speed, sadly we can’t just modify that component - to transform the entire tetrad is a little more involved. The standard method for this is something called a Lorentz boost (or more generally, a Lorentz transform - which may include rotations), which relates two observers moving at different speeds. A Lorentz transform in general relativity is often denoted by the symbol $\Lambda^i_{\;j}$, or $B^i_{\;j}$ for a Lorentz boost specifically here. This paper and this paper contain more information if you want to go digging
For us, we’re looking to perform a Lorentz boost in an arbitrary direction, and apply it to our basis vectors. Before we get there, we need to know what a 4-velocity is - something we’ve skimmed over a bit
4-velocities are not quite like 3-velocities
Lets imagine you have a regular good ol’ velocity in 3 dimensional space. We’ll scale our velocities so that $1$ represents the speed of light, and $0$ represents stationary relative to our observer. We’re going to examine the difference between:
- 3-velocities parameterised by coordinate time $\frac{dx^i}{dt}$, your regular everyday concept of velocity. We will call this $v$, and its euclidian magnitude is $\vert v \vert$. $\vert v \vert = 1$ represents light
- 4-velocities parameterised by coordinate time6 $\frac{dx^\mu}{dt}$
- 4-velocities parameterised by an affine parameter $\frac{dx^\mu}{d\lambda}$
- 4-velocities parameterised by proper time7 $\frac{dx^\mu}{d\tau}$
- Timelike vs lightlike geodesics, with all of the different parameterisations
It is common to define 4-velocities as only being those velocities which are parameterised by proper time, but we’re going with the generalised understanding here. Note that this segment is dealing with line elements in minkowski as that’s where we’ll be constructing our geodesics, and as such is special relativity. That said, the language of special relativity, and general relativity are often not very similar at all, so I’m putting this all down in our terminology
Lightlike Geodesics
A lightlike geodesic is defined has having $ds^2 = 0$. If you’ve forgotten, remember that we evaluate this quantity with the metric tensor, or directly with the line element
Coordinate time parameterisation
Constructing a 4-velocity for a lightlike geodesic which is parameterised by coordinate time is easy. Definitionally for a lightlike geodesic:
\[ds^2 = 0\]We can use the line element for minkowski as such, plugging in our 3-velocity to solve for the time component of a 4-velocity
\[\begin{align} ds^2 &= 0 = -dt^2 + dx^2 + dy^2 + dz^2\\ dt^2 &= \vert v \vert ^2 \end{align}\]We know a ray of light moves with a speed of $\vert v \vert=1$, therefore
\[dt = \pm 1\]Giving us a final coordinate parameterised 4-velocity of $\frac{dx^\mu}{dt} = (\pm 1, v^0, v^1, v^2)$
Affine parameterisation
This is the most common parameterisation for a geodesic, and the one we will be using. Luckily, because the parameter for a lightlike geodesic has no particularly useful interpretation8, we simply set $\lambda = t$ at the moment of construction
In minkowski, because spacetime is trivially flat, this parameterisation will always hold. In curved spacetime, this relation will only hold at the moment of construction, and then will diverge. This is because we use different geodesic equations depending on the parameterisation we pick
Proper time parameterisation
The full line element reads:
\[ds^2 = -d\tau^2 = g_{\mu\nu} dx^\mu dx^\nu\]For a lightlike geodesic, $ds^2 = 0$, so $d\tau^2 = 0$ ($d\tau$ being the change in proper time). There is therefore9 no proper time parameterisation of a lightlike geodesic. For this reason, it is common to state that the velocity of a lightlike geodesic is not a 4-velocity, as it can never be parameterised by proper time
Timelike Geodesics
A timelike geodesic is defined as when $ds^2 < 0$10
Coordinate time parameterisation
Lets first up construct a timelike 4-velocity $\frac{dx^\mu}{dt}$ parameterised by coordinate time. We know that the $dx^0/dt$ component must be $1$, as $dx^0 = dt$11. Lets check if $(1, v^0, v^1, v^2)$ is timelike:
\[ds^2 = -dt^2 + dx^2 + dy^2 + dz^2\\ \\ = -1 + dx^2 + dy^2 + dz^2 < 0\\\]Therefore, if $\vert v \vert < 1$, we do get a valid timelike geodesic $\frac{dx^\mu}{dt} = (1, v^0, v^1, v^2)$ parameterised by coordinate time
Proper time parameterisation
To transform from a coordinate time paramterisation, to a proper time parameterisation, we must multiply $\frac{dx^\mu}{dt}$ by $\frac{dt}{d\tau}$. How do we calculate $d\tau$? Easy, we use the line element for minkowski, and plug in our coordinate time velocity
\[\begin{align} ds^2 &= -d\tau^2 = -dt^2 + dx^2 + dy^2 + dz^2\\ -d\tau^2 &= -1 + \vert v \vert^2\\ d\tau^2 &= 1 - \vert v \vert^2\\ d\tau &= \sqrt{1 - \vert v \vert^2}\\ \frac{dt}{d\tau} &= \frac{1}{\sqrt{1 - \vert v \vert^2}}\\ \end{align}\]You may recognise this as the formula for the Lorentz factor $\gamma = \frac{dt}{d\tau}$. So to construct a 4-velocity parameterised by coordinate time from the 3-velocity $v^i$, we do:
\[\begin{align} \frac{dx^\mu}{d\tau} &= \frac{dt}{d\tau} \frac{dx^\mu}{dt}\\ \frac{dx^\mu}{d\tau} &= \frac{1}{\sqrt{1 - \vert v^i\vert^2}} \frac{dx^\mu}{dt}\\ \frac{dx^\mu}{d\tau} &= \gamma \frac{dx^\mu}{dt}\\ \frac{dx^\mu}{d\tau} &= \gamma (1, v^0, v^1, v^2)\\ \frac{dx^\mu}{d\tau} &= \gamma (1, v)\\ \frac{dx^\mu}{d\tau} &= (\gamma, \gamma v^0, \gamma v^1, \gamma v^2)\\ \end{align}\]Part of the reason why I’m spelling this out so explicitly is because all this notation is regularly used to mean the same thing, so hopefully you can come back to this in the future
Affine parameterisation
Like with lightlike geodesics, we can construct ‘an’ affine parameterisation by setting $\lambda = t$ at the moment of construction, after which the two parameters diverge. This however is very uncommon, and is only mentioned for completeness. When you do this, the parameterisation is hard to interpret physically12
We can also construct an affine time parameterisation by setting $\lambda = \tau$, where $d\tau = ds^2 = -1$. One very neat fact of proper time is that it is a general affine parameterisation, and so if we use a proper time parameterised geodesic and plug it through the geodesic equation specialised for the affine parameter (which is the one we use), it remains parameterised by proper time
Cat break

Calculating a Lorentz boost
We now know how to make an observer with a (timelike) 4-velocity in minkowski, by constructing it from a 3-velocity. To be very explicit, given a velocity in cartesian coordinates $d^i = (dx, dy, dz)$, where $\vert d\vert < 1$
\[\frac{dx^\mu}{d\tau} = v_{local} = \frac{1}{\sqrt{1 - |d|^2}} (1, d^0, d^1, d^2)\]We then want to convert $v_{local}$ to $v$ by transforming it with the tetrad, as $v^\mu = e_i^\mu v^i_{local}$, to get our new observer velocity in our curved spacetime
If we have an initial 4-velocity $u^\mu = e_0^\mu$ of our tetrad, and we want to boost the tetrad to represent an observer with a 4-velocity $v$, the formula for the Lorentz boost is this13:
\[\begin{align} B^i_{\;j} &= \delta^i_{\;j} + \frac{(v^i + u^i)(v_j + u_j)}{1 + \gamma} - 2 v^i u_j\\ \gamma &= -v_i u^i \end{align}\]$\delta^i_{\;j}$ is known as the kronecker delta. It is $1$ when $i==j$, and $0$ otherwise
Next up, we need to apply this Lorentz boost to our tetrad vectors. Lets say our original tetrads are $e_i^\mu$, and our boosted tetrads are $\hat{e}_i^\mu$. We already know what the new value of $\hat{e}_0^\mu$ will be, as it must be $v$, but the general transform is:
\[\hat{e}^i_a = B^i_{\;j} e_a^j\]Code
//gets our new observer
v4f get_timelike_vector(v3f velocity, const tetrad& tetrads)
{
v4f coordinate_time = {1, velocity.x(), velocity.y(), velocity.z()};
valuef lorentz_factor = 1/sqrt(1 - (velocity.x() * velocity.x() + velocity.y() * velocity.y() + velocity.z() * velocity.z()));
v4f proper_time = lorentz_factor * coordinate_time;
///put into curved spacetime
return proper_time.x() * tetrads.v[0] + proper_time.y() * tetrads.v[1] + proper_time.z() * tetrads.v[2] + proper_time.w() * tetrads.v[3];
}
//does the actual tetrad boosting
tetrad boost_tetrad(v3f velocity, const tetrad& tetrads, const metric<valuef, 4, 4>& m)
{
using namespace single_source;
v4f u = tetrads.v[0];
v4f v = get_timelike_vector(velocity, tetrads);
v4f u_l = m.lower(u);
v4f v_l = m.lower(v);
valuef Y = -dot(v_l, u);
///https://arxiv.org/pdf/2404.05744 18
tensor<valuef, 4, 4> B;
for(int i=0; i < 4; i++)
{
for(int j=0; j < 4; j++)
{
valuef kronecker = (i == j) ? 1 : 0;
B[i, j] = kronecker + ((v[i] + u[i]) * (v_l[j] + u_l[j]) / (1 + Y)) - 2 * v[i] * u_l[j];
}
}
tetrad next;
for(int a=0; a < 4; a++)
{
for(int i=0; i < 4; i++)
{
valuef sum = 0;
for(int j=0; j < 4; j++)
{
sum += B[i, j] * tetrads.v[a][j];
}
next.v[a][i] = sum;
}
}
return next;
}
Wormhole Results
With a wormhole with params M = 0.01, p = 1, a = 1, and an observer moving at 0.2c towards the wormhole:
Of course the foreground and background texture do not have to be the same, and can be distinguished by $l < 0$
M = 0.01, p = 1, a = 0.001
Redshift
The equations for redshift in general relativity are fairly straightforward. First off, we define the redshift14 $z$, as follows:
\[z+1 = \frac{g_{\mu\nu} k^\mu_{emit} u^\nu_{emit}}{g_{\mu\nu} k^\mu_{obs} u^\nu_{obs}}\]This is commonly also written:
\[z+1 = \frac{k^{\mu}_{emit} u_{\mu emit}}{k^\mu_{obs} u_{\mu obs}}\]$k^\mu$ represents our geodesic’s velocity, and $u$ is the observer’s velocity. $u^\mu_{emit}$ specifically will be where our ray terminates (and may either be the $e_0$ of a calculated tetrad, or in the case of eg an accretion disk - a known velocity), and $u^\mu_{obs} = e_0$ is our initial observer’s velocity (after boosting!). Do note that the metric tensors are evaluated at different locations
Next up, we need to work out how our light changes, from our end frame of reference (defined by $u^\mu_{emit}$), to our initial frame of reference. Light has two properties - frequency/wavelength, and intensity. The equation for wavelength looks like this15
\[z+1 = \frac{\lambda_{obs}}{\lambda_{emit}}\]Once we have our new wavelength, we need to calculate the intensity. We can do this by calculating the Lorentz invariant (constant in every frame of reference): $\frac{I_\nu}{\nu^3}$, where $\nu$ is your frequency, and $I_\nu$ is spectral radiance. See here 1.26 for details. Note that the quantity $I_\nu \lambda^3$ is also therefore Lorentz invariant
So, to calculate our observed intensity, we know that this quantity never changes, and can say:
\[I_{obs} \lambda_{obs}^3 = I_{emit} \lambda_{emit}^3\] \[I_{obs} = I_{emit} \frac{\lambda_{emit}^3}{\lambda_{obs}^3}\]This equation is linear in terms of intensity, which is often a useful property
Once we have our new wavelength(s) $\lambda_{obs}$, and $I_{obs}$, in theory we have everything we need to render our our final colour. We just have two unknowns, which are our initial intensity, and the initial wavelength(s)
Spectral Radiance
The $I_\nu$ that we’re dealing with in these equations is called spectral radiance - it is the power per unit frequency, and is not really a quantity that you often have in practice. Terminology here is confusing:
| Term | Meaning |
| Spectral Radiant Exitance | power per unit frequency per unit area |
| Spectral Radiance / Specific intensity / Spectral Radiant Flux | power per unit frequency |
| Radiant Exitance | power per unit area |
| Radiance / Radiant Flux | power |
If you want the equation for transforming a radiant flux, you’re looking for:16
\[F_{obs} = \frac{F_{emit}}{(z+1)^4}\]This is often much easier to work with, and is the quantity we get out of our accretion disk model later
Where do $I_{emit}$ and $\lambda_{emit}$ come from?
It depends what we’re simulating. For our use case - redshifting a galaxy background, you’d need frequency and intensity data across the entire sky. A good starting point is over here, luckily we live in 2024 and a significant amount of this information is simply public - unfortunately these skymaps do not come with what units their intensity data is in, making them unusable17. Still, you can go find the original surveys - though it requires significant digging which I’m not going to do in this article
If you have a blackbody radiator, it becomes fairly straightforward, as given a temperature we can redshift that directly, via the equation:
\[T_{obs} = \frac{T_{emit}}{1+z}\]For our galaxy background, we’re instead going to implement illustrative redshift, rather than attempting to find calibration data for hundreds of surveys - which I’ve had to try very hard to stop myself from doing
Illustrative redshift
Given that accurate skymap data is hard to find, I’m going to discard physicality when it comes to the colour, and just show a measure of redshift. We can still calculate $z+1$ as per normal, and then transform our radiant flux without needing to have a specific wavelength. The only thing we actually need wavelengths for is generating a final colour, but instead we’ll essentially just interpolate between red and blue with our $z$ value. When reading from a texture, our intensity data can be defined as the $Y$ component of the $XYZ$ colour space which represents energy, see here
\[Y = 0.2126 r + 0.7152 g + 0.0722 b\]Where $(r, g, b)$ is a linear sRGB colour. Once we’ve calculated our new intensity via the redshift equation, its then straightforward to perform a recolouring, and I’ll show an example below. $z$ has a range of $[-1, +\infty]$, so its easiest to split into two branches
Redshift Only (z > 0)
new_colour = mix(old_colour, pure_red / 0.2126f, tanh(z));
Redshift naturally fades to black as the intensity drops. The choice of tanh to map the infinite range to $[0, 1]$ is fairly arbitrary. See below for the explanation of the constant
Blueshift Only (z < 0)
iv1pz = (1/(1 + z)) - 1;
interpolating_fraction = tanh(iv1pz);
new_colour = mix(old_colour, pure_blue / 0.0722f, interpolating_fraction);
The mapping here is more complicated to replicate the same falloff as redshift. One question you might have is where these division constants come from: notice that they’re the same constants we use to calculate $Y$. This ensures that our new colour scales in brightness better - a pure white background colour will map to an equivalently bright blue colour, and darker colours will blend towards a brighter colour as our intensity increases. Without the division, a bright background colour would first darken as we mix in the visually less bright primary, before brightening again - this U bend in brightness is visually strange
One problem specific to blueshift is that our energy is unbounded, and our pixels can become infinitely bright. Its therefore much more aesthetically pleasing to spill over the extra energy into white once we max out the blue colour - which is shown in the full code sample
Code
This is one of those things that’s a lot easier to express in code, rather than equations:
//calculate Y of XYZ
valuef energy_of(v3f v)
{
return v.x()*0.2125f + v.y()*0.7154f + v.z()*0.0721f;
}
v3f redshift(v3f v, valuef z)
{
using namespace single_source;
{
valuef iemit = energy_of(v);
valuef iobs = iemit / pow(z+1, 4.f);
v = (iobs / iemit) * v;
pin(v);
}
valuef radiant_energy = energy_of(v);
v3f red = {1/0.2125f, 0.f, 0.f};
v3f green = {0, 1/0.7154, 0.f};
v3f blue = {0.f, 0.f, 1/0.0721};
mut_v3f result = declare_mut_e((v3f){0,0,0});
if_e(z >= 0, [&]{
as_ref(result) = mix(v, radiant_energy * red, tanh(z));
});
if_e(z < 0, [&]{
valuef iv1pz = (1/(1 + z)) - 1;
valuef interpolating_fraction = tanh(iv1pz);
v3f col = mix(v, radiant_energy * blue, interpolating_fraction);
//calculate spilling into white
{
valuef final_energy = energy_of(clamp(col, 0.f, 1.f));
valuef real_energy = energy_of(col);
valuef remaining_energy = real_energy - final_energy;
col.x() += remaining_energy * red.x();
col.y() += remaining_energy * green.y();
}
as_ref(result) = col;
});
as_ref(result) = clamp(result, 0.f, 1.f);
return declare_e(result);
}
For a Schwarzschild black hole, a velocity of 0.5c boosting towards the black hole, and a starting position of $(0, 5, 0, 0)$, you end up with this


From the front and back. Notice that we blueshift in the direction of travel, and see a redshift in the opposite direction. Do be aware that you should do all of this in linear colour, and only map your colours to sRGB right at the very end of your pipeline
Spinning black holes / The Kerr Metric
Accretion Disks
No black hole is complete without an accretion disk, so today we’re going to be looking at implementing a reasonable accretion disk model. We’re going to use whats called a thin-disk model (98-100), because it has a straightforward algebraic solution. In the future, we’ll be simulating accretion disks directly
One thing we should examine first is the concept of an innermost stable orbit, or ISCO for short
ISCO
The ISCO is the radius at which orbits around a black hole become unstable. Outside of this radius we can have long lived circular orbits - inside of this radius, circular orbits do not exist. This inner region is known as the ‘plunging’ region, and anything that’s within this region rapidly enters into a black hole
For a schwarzschild black hole, the ISCO is defined as $r_{isco} = 3rs = 6M$. For a Kerr (spinning) black hole, the ISCO is defined as follows18 for a black hole with mass $M$, and spin $a$:
\[\begin{align} X &= a/M\\ Z_1 &= 1 + (1-X^2)^{\frac{1}{3}} ((1+X)^{\frac{1}{3}}(1-X)^{\frac{1}{3}})\\ Z_2 &= (3 X^2 + Z_1^2)^{\frac{1}{2}}\\ r_{isco} &= M (3 + Z_2 \pm ((3 - Z_1)(3 + Z_1 + 2Z_2))^{\frac{1}{2}})\\ \end{align}\]The retrograde ISCO is higher than the prograde ISCO, so flip the sign appropriately when calculating
Accretion Disk Regions
Because orbits within the ISCO are unstable, matter depletes from this region very quickly. For this reason, accretion disks are often modelled as having a gap between the event horizon, and the ISCO - which we will follow19. For the model we’re looking at, here equations 98-100, we have three regions for us to work with, which are called:
- The inner region
- The middle region
- The outer region
Distinguishing between these three regions is done by two values
- Gas pressure vs radiation pressure. When gas pressure < radiation pressure, we’re either in the inner or outer region
- Whether opacity is driven by free-free interactions, or electron scattering. If free-free > electron scattering, we’re in the outer region, otherwise we’re in the inner or middle region
The details of this are interesting20, but we’re going to focus on the implementation. The general idea for us is to iterate from the innermost boundary of our accretion disk ($r = r_{isco}$), and terminate at some finite radius away from the accretion disk ($r = 100M$), working out which region we’re in as we go. We know at the start, we must be in region 1 - the inner region - at the ISCO
To distinguish when we transition from region 1, to region 2, which want to calculate (gas pressure / radiation pressure), and if its > 1 move into the middle region. This quantity is labelled $\beta / (1-\beta)$ (I do not know why)
To distinguish when we transition from region 2, to region 3, we calculate the quantity $T_{ff} / T_{es}$, which is the free-free opacity / the electron scattering opacity. When this quantity is > 1, we swap to region 321
Other details
To be able to implement this, we first need to calculate our spatial functions $A$ $B$ $C$ $D$ $E$ $Q_0$ $Q$, as well as $y_1$ $y_2$ $y_3$, and $y_0$. While not mentioned on the page we’re looking at, subscript $_0$ variables are evaluated at the ISCO. We do have an explicit formula for $Q_0$, which means that the only other one we need is $y_0 = (\frac{r_{isco}}{M})^{\frac{1}{2}}$
The meaning of the variables here are:
| variable | meaning |
| F | surface radiant flux (ie brightness) |
| $\Sigma$ | surface density |
| H | disk thickness |
| $\rho_0$ | rest mass density in the local rest frame |
| $T$ | temperature |
| $\beta / (1-\beta)$ | ratio of gas pressure to radiation pressure |
| $T_{ff}/T_{es}$ | ratio of free-free opacity to electron scattering opacity |
With this, we should have everything22 we need to implement this correctly
Code
The equations here - as written, are long and complicated to implement correctly. I won’t reproduce the equations algebraically in full here - it just introduces a risk of mistakes. You can find the full code for implementing this method, and producing a nice accretion disk texture over here
The core of our algorithm looks like this:
for(int steps = 0; steps < max_steps; steps++)
{
double r = mix(isco, outer_boundary, steps / (double)max_steps);
double x = sqrt(r/mass);
double r_star = r / mass;
double x_pow_m2 = mass/r;
double x_pow_m4 = pow(mass/r, 2.);
double A = 1 + assq * x_pow_m4 + 2 * assq * pow(x, -6.);
double B = 1 + a_star * pow(x, -3.);
double C = 1 - 3 * x_pow_m2 + 2 * assq * pow(x, -3.);
double D = 1 - 2 * x_pow_m2 + assq * pow(x, -4.);
double E = 1 + 4 * assq * x_pow_m4 - 4 * assq * pow(x,-6.) + 3 * pow(a_star, 4.) * pow(x, -8.);
double Q = B * pow(C, -1/2.) * (1/x) * (x - x0 - (3/2.) * a_star * log(x/x0)
- (3 * pow(x1 - a_star, 2.) / (x1 * (x1 - x2) * (x1 - x3))) * log((x - x1) / (x0 - x1))
- (3 * pow(x2 - a_star, 2.) / (x2 * (x2 - x1) * (x2 - x3))) * log((x - x2) / (x0 - x2))
- (3 * pow(x3 - a_star, 2.) / (x3 * (x3 - x1) * (x3 - x2))) * log((x - x3) / (x0 - x3)));
if(region == region_type::INNER)
{
///This is B/(1-B)
double p_gas_p_rad = 4 * pow(10., -6.) * pow(alpha, -1/4.) * pow(m_star, -1/4.) * pow(mdot_star, -2.) * pow(r_star, 21/8.) * pow(A, -5/2.) * pow(B, 9/2.) * D * pow(E, 5/4.) * pow(Q, -2.);
///in the edge region, gas pressure dominates over radiation pressure
///in the inner region, gas pressure is less than radiation pressure
///in the middle region, gas pressure is greater than radiation pressure
if(p_gas_p_rad > 1)
region = region_type::MIDDLE;
}
if(region == region_type::MIDDLE)
{
//in the outer region opacity is free-free
//in the middle region, opacity is electron scattering
double Tff_Tes = (2 * pow(10., -6.)) * (pow(mdot_star, -1.)) * pow(r_star, 3/2.) * pow(A, -1.) * pow(B, 2.) * pow(D, 1/2.) * pow(E, 1/2.) * pow(Q, -1.);
if(Tff_Tes >= 1)
region = region_type::OUTER;
}
double surface_flux = 7 * pow(10., 26.) * pow(m_star, -1.) * mdot_star * pow(r_star, -3.) * pow(B, -1.) * pow(C, -1/2.) * Q;
double T = 0;
if(region == region_type::INNER)
T = 5 * pow(10., 7.) * pow(alpha, -1/4.) * pow(m_star, -1/4.) * pow(r_star, -3/8.) * pow(A, -1/2.) * pow(B, 1/2.) * pow(E, 1/4.);
///'edge' region as well in the more developed model
if(region == region_type::MIDDLE)
T = 7 * pow(10., 8.) * pow(alpha, -1/5.) * pow(m_star, -1/5.) * pow(mdot_star, 2/5.) * pow(r_star, -9/10.) * pow(B, -2/5.) * pow(D, -1/5.) * pow(Q, 2/5.);
if(region == region_type::OUTER)
T = 2 * pow(10., 8.) * pow(alpha, -1/5.) * pow(m_star, -1/5.) * pow(mdot_star, 3/10.) * pow(r_star, -3/4.) * pow(A, -1/10.) * pow(B, -1/5.) * pow(D, -3/20.) * pow(E, 1/20.) * pow(Q, 3/10.);
radius.push_back(r);
brightness.push_back(surface_flux);
temperature.push_back(T);
}
This gives pretty nice results. For $M=1$23, $a=0.6$, $\dot{m} = 0.3$:

In practice you don’t need to use a 2d texture of an accretion disk - because its spherically symmetric, you could just take a radial slice
Colouring
One of the values we get out of our accretion disk model is a temperature $T$. If we assume that the accretion disk is a blackbody radiator, there’s a 1:1 mapping between every temperature, and the human perception of this colour. This forms a line across our colour space, and this relation from temperature to colour is known as the plankian locus. Working this out directly is nontrivial, though wikipedia also provides a useful approximation here. I’ve provided both of these methods over here, as I’d already implemented most of this in the past24
If you run the accretion disk temperatures through this process, you’ll be surprised to learn the colour of a real accretion disk:

(M = 1, a=0.99)
Rendering
Rendering the accretion disk is fairly straightforward. Because its modelled as a thin disk, you can check if a geodesic crosses the equatorial plane ($\theta = n\;\pi + \pi/2$), and sample the accretion disk texture. Here, I approximate the opacity as the brightness of the texture, because we’re not physically accurately raytracing this25, and do some very basic volumetrics on the disk
One key thing to note here is that we’re going to implement redshift, and to do that, we need to know the velocity of the fluid in the accretion disk. We already know that its moving approximately in circular orbits (otherwise it’d escape, or hit the black hole), but what is that as a velocity vector specifically?
Well, in the equatorial plane for circular orbits, we know that $dr = 0$, and $d\theta = 0$. This means that we’re only left to solve for $dt$, and $d\phi$.
Luckily other people have put in the legwork here, and here, and figured out that the angular velocity of a geodesic in the Kerr spacetime is
\[w = \frac{\dot{\phi}}{\dot{t}} = \frac{1}{r^{3/2} + a}\]Given that we know that our geodesic must point in the $d\phi$ direction, we can work out the $d\phi$ component as being $wr$. This means that $dt = d\phi/w = r$. We now have the 4-velocity of a geodesic on our equatorial orbit
Physically accurate redshifting
The nice thing here is that with the approximation that an accretion disk is a blackbody radiator, we can directly redshift the temperature26, and so end up with an accurate visual colour out of the other end:
\[T_{obs} = \frac{T_{emit}}{1+z}\]Given that mapping a temperature to a colour is an expensive process, I simply chuck the whole thing into a big buffer indexed by temperature, and call it a day
Code
#ifdef HAS_ACCRETION_DISK
valuef period_start = floor(position.z() / pi) * pi;
valuef in_start = cposition.z() - period_start;
valuef in_end = position.z() - period_start;
valuef min_start = min(in_start, in_end);
valuef max_start = max(in_start, in_end);
///we've hit the equatorial plane
if_e(pi/2 >= min_start && pi/2 <= max_start, [&]
{
valuef radial = position[1];
valuef M = BH_MASS;
valuef a = BH_SPIN;
///calculate the angular velocity
valuef w = pow(M, 1.f/2.f) / (pow(radial, 3.f/2.f) + a * pow(M, 1.f/2.f));
///calculate the real observer velocity
v4f observer = {radial, 0, 0, w * radial};
valuef ds = dot_metric(observer, observer, get_metric(cposition));
///valid timelike circular geodesic on the +r branch of kerr
if_e(ds < 0 && radial > 0, [&]
{
int buffer_size = 2048;
valuef outer_boundary = 2 * BH_MASS * 50;
valuef buffer_coordinate = (fabs(radial) / outer_boundary) * buffer_size;
v3f disk = lookup(accretion_disk, buffer_coordinate, 0.f, valuef(buffer_size - 1));
//if we've already hit another element of the disk, dim our contribution
disk = disk * clamp(1 - declare_e(opacity), 0.f, 1.f);
//add a fairly arbitrary amount of opacity to the tracing based on the brightness
as_ref(opacity) = declare_e(opacity) + energy_of(disk) * 50;
///change the parameterisation to proper time
observer = observer / sqrt(fabs(ds));
pin(observer);
#define ACCURATE_REDSHIFT
#ifdef ACCURATE_REDSHIFT
valuef temperature_in = lookup(temperature, buffer_coordinate, 0.f, valuef(buffer_size - 1));
///temperature == 0 is impossible in our disk, so indicates an invalid area
if_e(temperature_in >= 1, [&]
{
valuef zp1 = get_zp1(g.position, g.velocity, initial_observer, cposition, cvelocity, observer, get_metric);
///https://www.jb.man.ac.uk/distance/frontiers/cmb/node7.htm
valuef shifted_temperature = temperature_in / zp1;
valuef old_brightness = energy_of(disk);
///https://arxiv.org/pdf/gr-qc/9505010 12
valuef new_brightness = old_brightness / pow(zp1, 4.f);
///convert our temperature to a colour
v3f final_colour = lookup(bbody_table, shifted_temperature, 1.f, 100000 - 1.f) * new_brightness;
as_ref(colour_out) = declare_e(colour_out) + final_colour;
});
#endif
#ifdef RAW_DISK
as_ref(colour_out) = declare_e(colour_out) + disk;
#endif // RAW_DISK
if_e(opacity >= 1, [] {
break_e();
});
});
});
#endif
Interstellar’s other secret wormhole / Spinning black holes
A spinning black hole is generally modelled by the Kerr (or Kerr-Newman, with charge) metric. The interior of these metrics are actually pretty interesting. In addition to a ringularity (a ring singularity), the centre of a Kerr style black hole contains a wormhole, and copious time travel - which are certainly unusal things to find27. We’re going to take a trip inside!
The metric for a Kerr-Newman black hole in ingoing28 coordinates looks like this:
\[\begin{align} ds^2 = -(1-\frac{2Mr - Q^2}{R^2}) \;dv^2 + 2 dv dr - 2 a \frac{\sin^2 \theta}{R^2}(2 M r - Q^2)\; dv d\phi \\ - 2 a \sin^2 \theta \;dr d\phi + R^2\; d\theta^2 - \frac{\sin^2 \theta}{R^2}(\Delta a^2 \sin^2 \theta - (a^2 + r^2)^2)\; d\phi^2 \end{align}\]where
\[\begin{align} R^2 &= r^2 + a^2 \cos^2 \theta\\ \Delta &= r^2 + a^2 - 2 M r + Q^2 \end{align}\]$Q$ is our charge, $M$ is our mass parameter, and $a$ is the black hole’s spin
Kerr Metric Code
#define BH_MASS 1
#define BH_SPIN 0.99
metric<valuef, 4, 4> get_metric(const tensor<valuef, 4>& position) {
using namespace single_source;
valuef r = position[1];
valuef theta = position[2];
metric<valuef, 4, 4> m;
float M = BH_MASS;
float a = BH_SPIN;
valuef rs = 2 * M;
valuef ct = cos(theta);
valuef st = sin(theta);
valuef R2 = r*r + a * a * ct * ct;
valuef D = r*r + a * a - rs * r;
valuef dv = -(1 - (rs * r) / R2);
valuef dv_dr = 2;
valuef dv_dphi = -(2 * a * st * st / R2) * (rs * r);
valuef dr_dphi = -2 * a * st * st;
valuef dtheta = R2;
valuef dphi = -(st * st / R2) * (D * a * a * st * st - pow(a * a + r*r, 2.f));
///v, r, theta, phi
m[0, 0] = dv;
m[1, 0] = 0.5f * dv_dr;
m[0, 1] = 0.5f * dv_dr;
m[3, 0] = 0.5f * dv_dphi;
m[0, 3] = 0.5f * dv_dphi;
m[1, 3] = 0.5f * dr_dphi;
m[3, 1] = 0.5f * dr_dphi;
m[2, 2] = dtheta;
m[3, 3] = dphi;
return m;
}
This gives us a pretty nice looking black hole, which looks like this when rendered with an accretion disk (including redshift):
Parallel transport numerical accuracy
One thing to note is that the interior of Kerr is very numerically unstable, due to very high accelerations on the equatorial plane - it behaves very poorly in general. To make this article work, I had to upgrade the parallel transport code to be second order, to increase the accuracy sufficiently. This is a very basic second order integrator with nothing fancy otherwise:
v4f transport2(v4f what, v4f position, v4f next_position, v4f velocity, v4f next_velocity, valuef dt, auto&& get_metric)
{
using namespace single_source;
tensor<valuef, 4, 4, 4> christoff2 = calculate_christoff2(position, get_metric);
pin(christoff2);
v4f f_x = parallel_transport_get_change(what, velocity, christoff2);
v4f intermediate_next = what + f_x * dt;
tensor<valuef, 4, 4, 4> nchristoff2 = calculate_christoff2(next_position, get_metric);
pin(nchristoff2);
return what + 0.5f * dt * (f_x + parallel_transport_get_change(intermediate_next, next_velocity, nchristoff2));
}
Taking a trip into a spinning black hole
The ringularity in Kerr is extremely cool, and is one of my favourite things to simulate, so lets have a look at how this looks with an accretion disk!
Purrfect!
While I partly built this for the memes, its worth noting that the interior of a black hole and the wormhole itself is generally considered to be a mathematical artifact, and that it wouldn’t show up in reality. With that in mind, nobody really has a clue whats inside a black hole29!
The end

That’s the end of this small series of rendering arbitrary analytic metric tensors - there’s a lot more we could do here and I’ve been really crunching these articles down to the bones (possibly a bit too much). There’ll be articles in the future on this topic, but they’ll likely be on specific elements of this topic rather than the more broad approach I’ve taken here. The focus after this is largely going to be on numerical relativity - simulating the evolution of spacetime itself, and how to do that on a GPU
With that in mind, here’s the current list of topics that I’m going to get to in the future:
- Examining the BSSN equations and the ADM formalism in numerical relativity, to evolve some simple numerical spacetimes
- Binary black hole mergers
- Fast laplacian solving
- Gravitational wave extraction
- Approximate numerical raytracing
- Full numerical raytracing
- Stability modifications, and constraint damping
- Integrators for the EFEs
- Examining and calculating mass in GR
- Boundary conditions
- Particle system dynamics, including massless and massive accretion disks
- Investigating the hoop conjecture, mainly because its cool
- Negative energy in general relativity
- Relativistic eularian hydrodynamics
- Neutron star initial conditions, and equations of state
- Relativistic smooth particle hydrodynamics, which is a fun phrase to say
- Relativistic magnetohydrodynamics
- CCZ4/Z4cc/constraint damped formalisms, and friends
- Solving elliptic equations
On top of this, there are a number of misc topics to cover in analytic metrics:
- 4d Triangle rasterisation
- Time travel, and CTCs
- More interesting metric tensors, like the misner spacetime, cosmic strings, or analytic binary black hole metrics
- Near-massless (dust) particle systems
- Near-massless (dust) accretion disks
- Wave propagation in curved spacetimes
- 256x anisotropic texture filtering
- Relativistic volumetrics
This is going to take a hot minute to write up in a tutorially format - though its all largely work I’ve done previously (except smooth particle hydrodynamics, and magnetohydrodynamics). This kind of information doesn’t really exist outside of papers - and there are no gpu implementations - so it seems good to write it up
Until then, good luck!
-
Really this is more that this is a very Kip Thorne heavy article ↩
-
We’re using manhatten coordinate distance. You could use more advanced schemes - and these would work well, but bear in mind that calculating the timestep has a cost in itself and can end up having a significant overhead ↩
-
If you don’t know what this is: partially differentiate with respect to each variable (while holding the others constant, as per usual), and then sum all the resulting derivative. You should absolutely be automating this with dual numbers though! ↩
-
In practice I always take a trip spherical coordinates first, to fix velocity vectors when $r < 0$ (inverting dr) ↩
-
Unless you deliberately want to remove the effect of parallel transport on the camera’s pointing direction ↩
-
In minkowski, we have a time coordinate $t$ that we know is always a timelike coordinate, which is one of the major reasons the tetrad formalism is so useful. In general, in general relativity in arbitrary coordinates, we only have a coordinate system $(x^0, x^1, x^2, x^3)$ and it is not necessary that any of those coordinates represent time. This is why the $t$ in Schwarzschild coordinates is very misleading - it quite literally isn’t timelike everywhere in the metric ↩
-
I’m not sure we’ve defined this yet: proper time is the time as experienced by you, an observer floating through space. If you’re holding a clock, it is the amount of time elapsed on that clock. It has the symbol $\tau$ ↩
-
Note, this doesn’t mean you can completely freely reparameterise a lightlike geodesic. The equations for redshift rely on the geodesic at the start and end coordinates having the same parameterisation ↩
-
An alternative (and possibly better) argument is that the derivation of $ds^2 = -d\tau^2$ relies inherently on the geodesic being timelike, so $d\tau$ is simply undefined for lightlike rays and has no relation ↩
-
Do be aware that this is only true if we have a metric signature of [-, +, +, +] (which we use exclusively here), which corresponds to the signs in our minkowski line element. If you have a metric signature of [+, -, -, -], then a timelike geodesic would be defined as $ds^2 > 0$ ↩
-
Definitionally, $\frac{dx^\mu}{dt} = (\frac{dt}{dt}, \frac{dx}{dt}, \frac{dy}{dt}, \frac{dz}{dt})$ ↩
-
Because its still parameterised by an affine parameter, and proper time is an affine parameter, we can still consider it proper time - it just has a nonstandard scaling ↩
-
https://www.astro.ljmu.ac.uk/~ikb/research/zeta/node1.html ↩
-
This step is the bottleneck for actually achieving what we’re trying to do here. Try as I might, I cannot find any standardised way to obtain anything corresponding to physical units (instead of raw data in unknown units). If you know, please contact me! It looks like adadin may be able to do what we want, but its certainly not straightforward. Apparently the ‘default’ unit is ADU, which is the raw CCD readout data, but its not even vaguely clear how to go about converting this into a calibrated physical unit ↩
-
Note that one of the papers linked, this one, was originally what this article implemented, and claims to model the plunging region. This ended up being a significant delay, as as far as I can tell the equations for the plunging region do not work - you can straightforwardly show that the radial velocity profile is imaginary, and tends to infinity, simultaneously. This is a bit unfortunate ↩
-
If there was time, it would be interesting to lay it all out. This is one of the downsides of writing articles which are intended to be implementation focused, and a bit jumbo like this one. While the papers linked themselves contain all the theory you need, the thing we are lacking is actually how to implement this. In the future, I may revisit accretion disks in a lot more detail ↩
-
You should be aware that I’m not 110% certain that this is correct ↩
-
The equations we’re implementing mention the eddington luminosity. We don’t need this as we’re using a fraction of it, but you may want this for yourself, check out over here for details. I’ve added an implementation of this into the code sample as well ↩
-
Note that this is in geometric units ↩
-
My hobbies may not be the same as everyone else’s ↩
-
you have no idea how hard I have to resist this ↩
-
Redshifting a blackbody radiator has the surprising property that it represents another blackbody radiator at a different temperature, which feels unlikely but is apparently true ↩
-
I feel like at this point, physicists would be more happy if there were a library inside a black hole instead of singularities and time travel. I found out recently that almost no matter in a spinning black hole is actually ever able to hit the singularity - only strictly equatorial geodesics (if we’re talking timelike) can hit it, all other timelike geodesics just orbit about indefinitely or escape through the wormhole. Its a very strange place in there ↩
-
http://www.scholarpedia.org/article/Kerr-Newman_metric (47) (if you know a better reference than scholarpedia, please let me know - the website is a bit of a disaster), with signs flipped due to the metric signature. Do note that this coordinate system is unable to cover the whole path of our geodesic, as in general it will orbit the singularity - as it starts moving away from the singularity it’ll become singular. In reality we need to use multiple coordinate systems, but doing this performantly is tricky ↩
-
I sincerely hope that it is my cat though ↩